On the Physical Origin and Prediction of Killer Electron Storms

R. B. Sheldon, H. E. Spence, J. D. Sullivan,T. A. Fritz and Jiasheng Chen

Boston University Center for Space Physics
725 Commonwealth Av, Boston, MA 02215
18 May 1997




Abstract

Killer electrons with energies greater than 1 MeV are the main environmental hazard to Earth orbiting satellites, causing single event upsets (SEU) in logic or memory circuits and catastrophic high-voltage discharges due to deep dielectric discharges (DDD). The loss of the Telstar 401 communications satellite on January 11, 1997, was thought to be due to a DDD occurring 24 hours after a sudden, thousand-fold increase in killer electrons. Yet despite the ~40 years of work since the discovery of the outer radiation belts, the origin of killer electrons is still unknown. Measurements taken onboard the POLAR satellite this past year have revealed a population of 20--1500 keV electrons with pitch angles, 60Tsyganenko96 to demonstrate theoretically the trapping of keV electrons in the quadrupolar cusp region. Since electromagnetic fluctuations of the frequency and power adequate to pump up the energy of such a trapped population are known to exist in the cusp region, the cusp may possibly be the birthplace of outer radiation belt electrons. We study two recent storms that caused satellite failures to identify a plausible correlation of strong electric fields and cusp trapping with a DDD.



Introduction

 MeV electrons have been linked to numerous satellite failures, such as the January 10, 1997, event that may have led to a complete failure 24 hours later of a Telstar 401 communication satellite. Even after insurance, the loss cost AT&T over 100M SN97. Although some have found that the satellite failures occur in the declining phase of an MeV event and therefore question the direct connection, everyone is in agreement that a threshold, given by the total fluence of these penetrating electrons, is crossed in nearly every instance of satellite upset. Yet the origin and prediction of these killer electrons remain a mystery Baker97. Weak statistical links or neural net ``black boxes'' Koons91 are all we have found in the ~40 years since their accidental discovery by Van Allen [1968] \nocite{VanAllen68. What has been lacking is a physical model that directs the statistical investigation into fruitful correlations.

Where are these killer electrons and why is their origin a mystery? These MeV electrons are trapped in the Earth's dipole field, at a radial distance from ~\ 3--7 Re at the equator, forming the ``outer radiation belt''. As the Earth's dipole field weakens at larger distances, the fluctuations of the field caused by solar wind disturbances become increasingly important, so that the radial transport rate is faster than one Re per day at distances beyond 6 Re Schulz74. Beyond 8 Re, the dipole field is so distorted that it cannot trap the electrons at all, that is, they do not possess all three adiabatic invariants of the motion and therefore are at best ``pseudo-trapped'' Roederer70. Generally it is the third invariant that is violated most easily, meaning that the electrons cannot drift 360 degrees around the Earth without encountering the magnetopause and becoming lost. Thus if the source of killer electrons is not in the trapping region itself, it would appear to be a transient in the outer regions, having a lifetime of several tens of minutes, the time it takes for electrons to drift around the Earth. Yet extensive searches in the trapping region have shown no acceleration region or population that can be the source of killer electrons (e.g., a ``Nishida recirculation'' type mechanism Paulikas79,Nishida76).

Recent work using SAMPEX has confirmed what other data sets have been telling us, that the phase space density at constant magnetic moment uniformly rises toward higher L-shells, away from the Earth. Since the diffusive radial transport rate for these electrons is rapid, this suggests that the source is external to the trapping region. However, the solar wind (at infinite L-shell) has a lower phase space density than the magnetosphere whether we compare at constant energy or constant magnetic moment Li96. Thus until recently we could only say that the mysterious source of these killer electrons lies at 10Li93), yet remain for many hours while filling the radiation belts. No one has.


Data Analysis

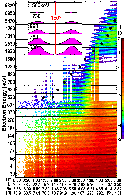 FIGURE 1: Electrons trapped in the cusp observed by POLAR. See text for details.

Another, previously unexamined possibility exists, that there may be a trapped population at large L-shells whose trapping does not depend on the usual dipolar magnetic bottle geometry. If this population exists, it could account for the greater phase space density seen at higher L-shells as well as provide a location for slow, steady acceleration to occur. And that is what we have found. The recent discovery of energetic electrons quasi-trapped in the cusp has provided a fortuitous glimpse of what we believe to be the birthplace of these killer electrons.

We have stumbled, like Van Allen, into a place or onto a mechanism that stores and produces these MeV electrons, observing trapped particles in the Earth's cusp. In Figure \ref{polar} we plot time-energy-pitchangle-count spectrograms from the CEPPAD/HIST electron instrument Blake95,Contos97 on the POLAR spacecraft, which is in a 2x9 Re orbit that on October 14, 1996, passed through the nominal cusp before traversing the radiation belts. This is just one of the >100 such examples we could have shown, since we observe this population whenever the POLAR orbit precesses through the cusp region. The bottom panel shows the radial distance and L-shell as a function of time plotted logarithmically from 2--20 Re. Successive panels from the bottom are .52, .63, .78, .99, 1.23, 1.5, 1.92, 2.53, 3.31, 4.28, 5.47 MeV electron energies, where each panel displays the roll modulation (pitch angle) of the particles; the dotted black and bracketting blue lines in every panel show the 90 degrees and 60 degrees pitch angle sectors with respect to the magnetic field. Clearly the fluxes are peaked around 90 degrees. The color scale displays the logarithm of the countrate from 1 (purple) to 10,000 (red). White vertical stripes are data loss due to telemetry mode. The left half of the plot shows 0.5--1.5 MeV electrons with quasi-trapped pitch angle distributions located in the cusp at L>10. The right half of the plot is an outer radiation belt traversal with the ``slot'' region of weaker flux seen at the lowest L-shells. Comparing the radiation belt and cusp loss cones, we see that the cusp's is much wider and the fluxes more isotropic, which is characteristic of a ``leaky magnetic bottle''.

Now this quasi-trapped cusp population is highly unusual because, classically speaking, the cusp cannot trap particles Roederer70, it is not an ``excluded region'' in the St\"ormer theory of an idealized dipole Stoermer11,Rossi70. However, the interaction of a magnetic dipole with the solar wind modifies the topology in a fundamental way that has not been adequately considered in the theory of trapped particles. Rather than a dipole, the cusp appears to be a quadrupole, resembling a Paul or Penning trap (which recently demonstrated Bose-Einstein condensation PT97). We demonstrate the existence of such a quadrupolar trap using the somewhat extreme geomagnetic conditions of a nearly minimum latitude cusp and a high speed solar wind (figure \ref{trap}).

Simulations

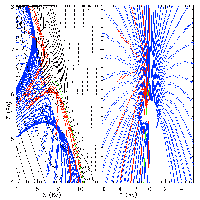 FIGURE 2: Trajectories of trapped 1 MeV electrons in the the Earth's outer cusp, projected into the GSM X-Z and Y-Z planes. Dashed lines are field lines from the T96 magnetic field model (Dipole: June 21, 1996, 1300UT; Solar Wind: +10nT Bz, 1/cc, and 1000km/s V_SW). Black lines are contours of |B| in nT. Blue trajectory completes a full drift orbit; red trajectory escapes poleward after a half-drift, green trajectory (started near the cusp center) never completes a bounce.

When we trace particles through this region we find trapping to occur when the electrons mirror around the local minimum of the field line found at the center of the cusp. The orbits take the shape of a flower petal, with a locally outward magnetic gradient instead of the typical inward gradient so that the particles drift in an opposite sense to the trapped radiation belt particles. Our preliminary results show that 5--350 keV electrons can be trapped in the cusp of a T96 magnetosphere though admittedly without an electric field (see Figure \ref{trap}). Examination of particle trajectories in this region show that although they lack a standard second and third invariant, since they never cross the magnetic equator, yet if we define a ``cusp equator'' as the surface of minimum |B| along a field line that approaches the cusp, we can then define clearly analogous second and third invariants of the motion. Thus we can uniquely identify these invariants in analogy to B-L space by their pitch angle and |B| at the crossing of the ``cusp equator''. In figure \ref{trap} one can see 3 nested ``cusp-shells'' analogous to L-shells of the dipole. The limiting 2nd invariant of these trapped orbits occurs when the mirror point |B_m| approaches the dayside equatorial field strength, at which point the electrons join the dipolar pseudo-trapped population and grad B drift away from the cusp. From the pitch angle distribution, this value appears to be around 60 degrees. The limiting 3rd invariant is the maximum value of |B| for which the ``cusp equator'' is still defined over a closed, 360 degree loop.

A Theory of Cusp Acceleration

 How does this cusp trap produce killer electrons? As others have shown Delcourt92, the magnetic moment of these trapped electrons need not be conserved as they pass near the minimum B-field point. Thus the electrons may change their energy in a random fashion, diffusing in energy space by ``stochastic'' acceleration. The trajectory outside the magnetopause in figure \ref{trap}, shows just such a stochastic pattern probably due to asymmetries in the quadrupole trap. That is, near the minimum field point, the length scales (and time scales) of the adiabatic invariants converge, leading to a ``Arnol'd web'' in phase space, and rapid stochastic acceleration Arnol'd64. These MeV electrons escape the trap and diffuse into the radiation belts, adiabatically gaining energy from ~1 MeV to ~5 MeV in the process.

Does this trap hold the electrons long enough for such an indirect acceleration process to raise them up to MeV energies? Since all electrons look the same, we turn to solar wind ions as a ``tracer'' of particle trapping. On May 29, 1996, the POLAR/CAMMICE instrument observed solar wind O^6+ ions deep in the cusp, nearly 2 hours after a brief interlude of Bz southward in the midst of a strongly Bz northward solar wind stream Grande97. We then scale the 500 keV oxygen ion to a 5 keV electron, and conclude that electrons are trapped in the cusp for at least 30 minutes. Using the Bohm diffusion rate as an upper limit on stochastic acceleration, we calculate that this same 5 keV electron will reach 1 MeV energies in the presence of a static 20 mV/m cusp electric field (observed by POLAR/EFI) in about 4 seconds. Thus we appear to have plenty of time for stochastic acceleration to operate on this trapped population.

Then why doesn't the cusp trap keep the outer radiation belt constantly full of killer electrons? Most probably because the efficiency of the mechanism has large time variations. Stochastic acceleration is dependent upon a minimum energy ``seed population'', which is not always available in the shocked magnetosheath plasma. That is, when electric fields are superposed on the cusp trap there may exist a minimum energy electron at which grad B drifts dominate over ExB and permit trapping. The trap may also be capable of positive feedback, so that sufficient trapped plasma deepens the diamagnetic cavity and enhances the trapping time, which we surmise to be the case for the May 29 or Aug 27, 1996 events Chen97. Such positive feedback can generate large variations from small perturbations so that the trapping efficiency should depend strongly on the magnetic geometry. The acceleration mechanism may also be highly time-variable depending on reconnection rates or variations in the solar wind pressure. With so many degrees of freedom, it is difficult to make theoretical progress without empirical data. Therefore we examine two events that caused satellite failures, and relate the data to the best models we presently have.

Anik & Telstar Killer electron Events

 Because of the ~\ 24 hour delay between a magnetic storm and the onset of killer electrons, it seemed reasonable to use geomagnetic indices, such as Dst or Kp, to predict an MeV electron enhancement. However, the correlation is very weak, particularly with Dst. For example, the largest MeV enhancement in 1996 occurred on April 15, with a Dst response of of no more than -70nT. The largest Dst storm in 1996 was -110 nT on October 23, which caused a decrease in the overall MeV content of the radiation belts. This was most disturbing, suggesting that the strongest acceleration mechanism we know, which energizes the ring current during geomagnetic storms, is uncorrelated or anticorrelated with the production of MeV electrons.

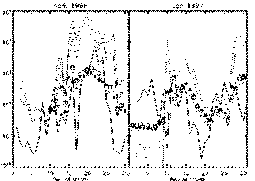Predicted (solid line) and actual fluxes (dashed line) of >3MeV electrons from the daily peak of the GOES electron channel for the week of April 15, 1996, and January 10, 1997. GOES 7,8 & 9 were available in April, only 8 & 9 were available in January. Symbols are 1.1-1.5 MeV electrons from the Los Alamos detector. Data sets were normalized to the Koons prediction by applying a constant scaling.

Recently, Nagai88 presented a linear filter that had much better success correlating MeV electrons with Kp than with Dst. Koons91 generalized this approach to a non-linear filter or neural net. With the neural net they were able to predict 70\% of the variation in MeV electrons. But the question remained, can it predict the onset of a killer electron enhancement? Two enhancements were tested using the neural net, April 15, 1996, and January 10, 1997; both having little Dst response and both causing geosynchronous spacecraft failures. (April 15 was the last of a 27-day recurring storm in which the Anik 1 & 2 satellites failed during the previous Carrington rotation, but at a weaker killer electron flux level.) The results are plotted in figure \ref{koons}, along with the >3MeV electrons from GOES 7,8 \&9, and the 1.1-1.5 MeV electrons from the Los Alamos satellites. In both cases, the neural net fails to predict the onset time or the intensity, though to its credit, it does recognize the April event as a major killer electron event.

From this comparison we make several observations. MeV electron enhancements are characterized by a hardening of the spectrum. There appears to be strong LT asymmetries in the onset of these storms, as well as a more abrupt onset than expected from the neural net trained on 1984 storms. The April 15 event triggered Koons' ``red'' limit, but the January event barely touched the Koons' ``yellow'' limit. The lack of a Dst signature may be correlated to the presence of a strong asymmetry seen both in the magnetograms (ASY) and in the GOES electron data.

Discussion

 If the cusp is indeed the source of killer electrons, how can it account for the signatures observed in our two case study? The secret lies in the lack of a Dst response. In both cases, something happened to the magnetosphere on a timescale that was faster than the time required to set up a stable ring current. Although the effect was the same on the unfortunate satellites, their causes were quite different, so we address these two situations separately.

From ISTP measurements on April 15 Sheldon97b, we know that an intense, 150kV cross-polar cap potential was in place for a short 3 hours, when Bz turned strongly southward to -10nT, and simultaneously the solar wind jumped from 400 to 600 km/s. These extreme conditions caused the plasmasheet ions to convect rapidly through the magnetosphere, rather than lingering in the ring current where they would otherwise cause a Dst response. Meanwhile the strongly negative Bz southward eroded the dayside subsolar magnetopause to the point that the cusp was tilted into the ram direction of the solar wind. When the cusp was sufficiently aligned, we surmise that conditions became ideal for the trapping of electrons in the cusp. This trapping, coupled with the large electric fields available at the time, proved to be an efficient mechanism to accelerate the electrons to MeV energies much faster than usual.

January 10 was a much quieter and surprisingly benign solar wind environment. A very small shock, raising the solar wind speed from under 400 to barely 450 km/s, occurred around 0100 UT during a northward Bz time period. Dst responded weakly at first because not all the ingredients for a classic storm were present, namely a strong Bz southward component coupled with a high speed solar wind. Four hours into the event, around 0500 UT, the magnetic cloud proper arrived at a very slow speed of about 450 km/s with a rotation of the IMF strongly southward until 1800 UT. What is surprising is that the MeV electrons jumped from barely measurable to moderately high in less than 12 hours. This enhancement was highly transient, appearing as a 3 hour spike in GOES 9, and as a suspicious data gap in GOES 8. Simultaneously, POLAR/CEPPAD energetic neutral atoms recorded a highly asymmetric ring current, suggesting a substantial electric field, perhaps generated from the large rotation of IMF Bz. The best clue was that the weak shock arrived at the Earth around 0100 UT, approximately 3 hours before the southern cusp had rotated to its minimum latitudinal extent during winter solstice. We surmise that this fortuitous cusp orientation, coupled with a very slight solar wind shock, produced a much greater than normal trapping of electrons. Unlike the April 15 event, the acceleration appeared to begin several hours after the trapping, since at 0500 UT the radiation belt passage of POLAR showed no enhancements. But by 2000 UT, the IMF Bz had rotated, electric fields were present, and the radiation belts had jumped in intensity by 3 orders of magnitude. Thus we would argue that both a trapping geometry and an acceleration electric field appear to be necessary for the generation of killer electrons. The abrupt decay of this event from its maximum suggests that a 450 km/s solar wind isn't fast enough to maintain constant trapping, even in a highly tilted cusp. The arrival of a second shock on 11 January with higher solar wind speeds may have caused a slight increase in the MeV electrons, but it was not accompanied by southward Bz, and thus was not as effective as the first shock.

Why should the rather mild Jan 10 MeV event have caused a total satellite failure? It may be that the DDD events are not as much caused by killer electron fluence as by changes in that fluence. That is, although the MeV electrons deposit charge into dielectrics which can potentially lead to deep dielectric discharges, they are also enhancing the leakage current through dislocations and ionization in the dielectric. When such MeV enhancements start or stop suddenly, the slower discharge cannot keep up with the fast charging process and catastrophic sparking may occur. The abruptness of these MeV enhancements is magnified if there are strong LT asymmetries in the flux which when coupled to the satellite orbital speed, may cause even faster temporal changes in the flux. Thus it would be as important to know the spatial distribution and the time rate of change of these enhancements as it is to know their magnitude.

Conclusions

 We have shown that the POLAR spacecraft observed quasi-trapped MeV electron distributions in the Earth's cusp, and that these distributions are consistent with trapped electrons in the cusp simulated using the Tsyganenko 96 model. Although the trapping is quite different than the standard dipole trapping geometry, we show that an analogous 3 invariants of the motion exist for this trapped population as well. We show that trapping alone or electric fields alone are not sufficient to produce a killer electron response, but in concert are very effective at accelerating electrons to MeV energies. The presence of an asymmetric ring current may be correlated to a strong electric field which caused the sudden production of MeV electrons, as well as its effectiveness in producing DDD in spacecraft. Therefore, if cusp trapping and energization can be established as the origin of killer electrons, it would be a major breakthrough in space weather and permit the specification and prediction of the major natural hazard to Earth orbiting satellites.

Acknowledgements

 This study was supported by NASA contract NAS5-97147. We gratefully acknowledge the POLAR/CEPPAD data provided by B. Blake, and the geosynchronous electron data provided by G. Reeves.

References

TOC Comments? r*bs@rbsp.info
(due to spamming, delete the asterisk)