On the Physical Origin of Outer Radiation Belt 1--10 MeV Electrons

R. B. Sheldon, H. E. Spence, J. D. Sullivan,T. A. Fritz and Jiasheng Chen

Boston University Center for Space Physics
725 Commonwealth Av, Boston, MA 02215
October 1997

Abstract

We report on the POLAR/CEPPAD discovery of a trapped, 60 to demonstrate theoretically the trapping of these energy electrons in the outer cusp region and the resonant frequencies of its trapped motion. We argue that the large phase space densities observed there are sufficient to fill the outer radiation belts with 1--10 MeV electrons. The origin of these electrons is still unknown despite the ~40 years of work since the discovery of the outer radiation belts. During the equinoxes, the POLAR orbit passed through the outer cusp as well as the radiation belts, and observed increases in the trapped cusp electrons which were correlated with increases in the radiation belt electrons. Since electromagnetic fluctuations of the appropriate resonant frequency and power adequate to pump up the energy of such a trapped magnetosheath population are known to exist in the cusp region, the cusp may possibly be the birthplace of outer radiation belt electrons.

Introduction

 Large fluxes of 1--10 MeV electrons which define the outer radiation belt, may pose a significant environmental hazard to geosynchronous satellites, yet the origin and prediction of these electrons remains a mystery Baker97. In particular, the order-of-magnitude flux enhancements that have characteristic rise times of 0.5--2 days are especially difficult to predict. Weak statistical links Blake97 or neural net ``black boxes'' Koons91 are all we have found in the ~40 years since their accidental discovery by Van Allen [1959] \nocite{VanAllen59. What has been lacking are physical models that direct the statistical investigation into fruitful correlations that might create better predictors of these MeV electron enhancements.

Where are these electrons and why is their origin a mystery? These MeV electrons are trapped in the Earth's dipole field, at a radial distance from ~ 3--7 Re at the equator, forming the outer radiation belt. As the Earth's dipole field weakens at larger distances, the fluctuations of the field caused by solar wind disturbances become increasingly important, so that the radial transport rate is faster than one Re per day at distances beyond 6 Re Schulz74. Beyond 8 Re, the dipole field is so distorted that it cannot trap the electrons at all, that is, they do not possess all three adiabatic invariants of the motion and therefore are at best ``pseudo-trapped'' Roederer70. Generally it is the third invariant that is violated most easily, meaning that the electrons cannot drift 360 degrees around the Earth without encountering the magnetopause and becoming lost. Thus if the source of the electrons is not in the trapping region itself, it would appear to be a transient in the outer regions, having a lifetime of several tens of minutes, the time it takes for electrons to drift around the Earth. Yet extensive searches in the trapping region have shown no acceleration region or population that can be the source of the outer zone electrons (e.g., a ``Nishida recirculation'' type mechanism Ingraham94,Paulikas79,Nishida76).

Recent work using POLAR has confirmed what other data sets have been telling us, that the phase space density, f, at constant magnetic moment uniformly rises toward higher L-shells, away from the Earth during quiet conditions Selesnick97. However during more active times, f can show multiple peaks in the outer zone. Since the diffusive radial transport rate for these electrons is increasingly rapid with L-shell, this suggests that a time-variable source/sink external to the trapping region is consistent with both observations, whereas an internal source, whether steady or time-variable, is inconsistent with the quiet-time profile. However, the solar wind (at infinite L-shell) has a lower phase space density than the magnetosphere whether we compare at constant energy or constant magnetic moment Li97. Thus until recently we could only say that the mysterious time-variable source of these electrons lies at 10Li93), yet unlike the shock mechanism, remain for many hours while filling the radiation belts.

Another, previously unexamined possibility exists, that there may be a trapped population at large L-shells whose trapping does not depend on the usual dipolar magnetic bottle geometry. If this population exists, it could account for the greater phase space density seen at higher L-shells as well as provide a location for slow, steady acceleration to occur. And that is what we have found. The recent discovery of energetic electrons trapped in the cusp has provided a fortuitous glimpse of what we believe to be a suitable birthplace of these electrons, which then populate the outer radiation belts.

Data Analysis

 POLAR is in a 2x9 Re orbit that on October 14, 1996, passed through the nominal outer cusp before traversing the radiation belts. The outer cusp is defined to be a region inside and adjacent to the magnetopause (8--10 Re), with noticeably reduced magnetic field strengths, having broadband wave power, and generally within some radial distance (2--3 Re) of the topological minimum B point. We do not define the outer cusp with respect to a particle population for the same reason that the plasmasphere, radiation belts, and ring current define overlapping regions in the dipole magnetosphere. We observe a trapped electron population in the outer cusp on this orbit, generally during the two seasons per year when the POLAR orbit precesses through this region. Data from TIMAS and HYDRA on this day show that the magnetopause was first crossed at 0100, at which time EFI showed an abrupt increase in broadband noise. HYDRA showed brief bursts of sheath electrons between 0100--0230 that appeared to be anti-correlated with IES and HIST trapped electrons. These short magnetopause crossings ceased by 0230 along with most of the EFI wave power.

In Figure \ref{polar} we plot time/energy/roll-angle spectrograms of phase space density from the CEPPAD/HIST and CEPPAD/IES electron instrument Blake95,Contos97 on the POLAR spacecraft. The vertical stripes in the upper panels are an instrument artifact caused by mode switching of the HIST telescope. Successive panels are logarithmically spaced in energy where each panel displays the roll modulation (pitch angle) of the particles; the fluxes are clearly peaked around 90 degrees. The color scale displays the logarithm of f (s^3/km^6) from 0.00001 (purple) to 100 (red). The left half of the plot shows 30--1000 keV electrons with trapped pitch angle distributions located in the outer cusp at L>10. The right half of the plot is an outer radiation belt traversal. Comparing the radiation belt and cusp loss cones, we see that the cusp's is much wider, which is characteristic of a ``leaky magnetic bottle''. It also appears that the wide loss cone of the cusp is filled at a very low, isotropic level. Comparing the phase space densities at equal magnetic moment (keV/nT), which involves connecting the two regions by a diagonal line roughly parallel to the isodensity contours of the radiation belts, reveals that the outer cusp has higher densities than the outer radiation belts, allowing the possibility of inward diffusion at constant first invariant. Note that the radiation belt pass is at high latitude so that the electron flux would map into the wide loss cones of the outer cusp, suggesting that the second invariant is not conserved if the cusp is the source of these electrons.

In Figure \ref{october} we plot counts vs energy of the same channels displayed in the HIST detector (upper half of Fig. \ref{polar}) on 32 successive passes of the cusp and radiation belts occurring in October 1-24, 1996, during which the MLT of the POLAR orbit passed very close to noon. The color scale extends from 1 (purple) to 100,000 (red). Each panel is the dayside pass when L<20, with geosynchronous orbit occurring nearly in the center of each panel, and the slot region at minimum L~3 occurring in the final third of the panel. From Figure \ref{polar}, we can identify the cusp as the non-zero fluxes of MeV electrons observed outside of L=10. Since they occur on nearly every orbit (on every orbit if we use a more sensitive singles rate), we infer that the cusp always has a residual trapped population. Although the correlation is not perfect, one can see that the intense cusp fluxes observed on Oct 14 precede by 35 hours an enhancement seen in the radiation belts on Oct 16. The cusp enhancement on Oct 16, though equally as intense as the 14th, produced a much smaller but measurable increase on the 18th. However the three consecutive cusp enhancements of the 18-19 produced a growing radiation belt enhancement on the 20th. This suggests that the cusp may fill the radiation belts best when given a few days of constant cusp activity.

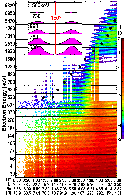FIGURE 1: Electrons trapped in the cusp observed by POLAR. See text for details.

Simulations

 Now this trapped cusp population is highly unusual because, classically speaking, the cusp cannot trap particles Roederer70, it is not an ``excluded region'' in the St\"ormer theory of an idealized dipole Stoermer11,Rossi70. However, the interaction of a magnetic dipole with the solar wind modifies the topology in a fundamental way; rather than a dipole, the cusp appears to be quadrupolar. We demonstrate the existence of this particle trap using the geomagnetic conditions of a nearly minimum latitude cusp and a nominal 10 Re standoff distance (figure \ref{trap}).

When we trace particles through this region we find trapping to occur when the electrons mirror around the local minimum of the field line found at the center of the cusp. The orbits take the shape of a lily, with a locally outward magnetic gradient instead of the typical inward gradient so that the particles drift 360 degrees around the cusp in an opposite sense to the trapped radiation belt particles. Our results show that 5--6000 keV electrons can be trapped in the cusp of a T96 magnetosphere for tau>300 seconds (i.e., many drift orbits), though admittedly without an electric field (see Figure \ref{trap}). Examination of particle trajectories in this region shows that although they lack a dipolar second and third invariant, since they never cross the dipole magnetic equator, we can find an analogous second and third ``cusp'' invariants of the motion if we define the ``cusp equator'' to be the surface of minimum |B| along a field line that approaches the cusp. Thus we can uniquely identify these invariants in analogy to a dipole by their pitch angle and |B| at the crossing of the cusp equator. In figure \ref{trap} one can see two nested ``cusp-shells'' analogous to L-shells of the dipole. The limiting 2nd invariant of these trapped orbits occurs when the mirror point |B_m| approaches the dayside equatorial field strength, at which point the electrons join the dipolar pseudo-trapped population and grad_B drift away from the cusp. From the pitch angle distribution, this value appears to be alpha0~60 degrees. The limiting 3rd invariant is the maximum value of |B| for which the ``cusp equator'' is still defined over a closed, 360 degree loop.

Can these particles have come from the tail, are they topologically connected to the nightside trapped particles that have drifted into the bifurcated dayside minimum? Yes, they are physically in the same region of space, but separated in phase space by very different second invariants. Take for example a 50 keV 90 degree pitchangle particle in the outer cusp, mirroring at 25 nT. For it to maintain the same magnetic moment while drifting, it must find a region of the magnetosphere with <25 nT fields. The only other such region is deep in the tail, and topologically disconnected from the cusp, so that the particles remain trapped in the cusp and cannot drift away without destroying their first invariant. Conversely a 50 keV 90 degree pitchangle particle trapped at midnight in a 50nT field can mirror through the cusp, but its pitchangle when at the 25 nT level must be 30 degree. Thus the faint background level inside the wide cusp loss cones could be understood as dipole-trapped particles, but the peak at 90 degree can only be locally trapped.

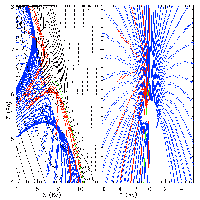FIGURE 2: Trajectories of trapped 1 MeV electrons in the the Earth's outer cusp, projected into the GSM X-Z and Y-Z planes. Dashed lines are field lines from the T96 magnetic field model (Dipole: June 21, 1996, 1300UT; Solar Wind: +10nT Bz, 1/cm^3, and 1000km/s V_SW). Black lines are contours of |B| in nT. Blue trajectory completes a full drift orbit; red trajectory escapes poleward after a half-drift, green trajectory (started near the cusp center) never completes a bounce.

Discussion

 How would this cusp trap accelerate electrons? As others have shown Delcourt92, the magnetic moment of these trapped electrons need not be conserved as they pass near the minimum B-field point. Now in the absence of an electric field, such a ``scattering'' event leads only to a change in pitch angle, or a circular constant energy surface in v-perp - v-parallel space. However when a DC or an AC electric field is present, energy may be gained or lost. One example is anomalous or Bohm diffusion. If the cusp has a DC electric field of about 1 mV/m (typical values as inferred from flows measured by POLAR/TIDE), then a ~30 kV potential exists across the cusp. If the electron gyrates 180 degree, and scatters by 180 degrees successively, it can gain 30 keV of energy from the global electric potential as it crosses the cusp, which being perpendicular energy, modifies its first invariant. If the particle is then allowed to drift without scattering, returning to its original position, it can undergo the same process repeatedly, gaining energy up to the trapping limit of the cusp. Note that the full 1 MeV potential is not needed to accelerate the electrons in a single step, rather a recirculating, multi-step acceleration can reuse the same potential many times. Eventually these MeV electrons escape the trap (perhaps by becoming too energetic to remain trapped) and diffuse into the radiation belts, adiabatically gaining energy from ~1 MeV to ~5 MeV in the process. Naturally, both drift and scattering are occurring simultaneously, so that the energy changes by small steps rather than in the large steps described above.

Now the crucial feature of the Bohm diffusion example above (in addition to an electric field) is that there exist a ``scattering'' mechanism with a period resonant with the gyration period. One could invoke a whole plethora of resonant mechanisms, each based on one of the three frequencies associated with adiabatic invariants (e.g., radiation belt acceleration is resonant with the drift motion). Yet even with a resonance, it takes many steps, uncorrelated with each other, to accelerate the particles, so that the electrons change their energy in a random fashion, diffusing in energy space by ``stochastic'' acceleration Fermi49.

In addition to resonant stochastic acceleration, if two (or three) of the adiabatic periods nearly overlap, then the phase space density changes even more chaotically, such that stochastic acceleration is most effective when the frequencies associated with each adiabatic invariant are nearly commensurate. If the cusp supports chaotic motion, then particle acceleration can occur even more rapidly than the simple diffusion theory described above. In the dipole trap, these periods are separated by timescales of 100-1000, and chaotic behavior does not appear. However the cusp trap is an ``inside-out'' dipole, so that near the minimum field point, the time scales of the adiabatic invariants converge, (see Table 1), allowing the possibility that large enough fluctuations will generate chaotic motion, an ``Arnol'd web'' in phase space with rapid chaotic (also sometimes called stochastic) acceleration Arnol'd64. The correlation of MeV electrons with high speed solar wind Blake97 may then be due to more than just the higher fluctuation power in such a solar wind, which delivers more power at the resonant frequencies of the electrons, but also due to the onset of non-linear chaotic behavior.

Does this trap hold the electrons long enough for such an indirect acceleration process to raise them up to MeV energies? Ideally we would tag some cusp electrons and observe their trapping times, but since all electrons look the same, we turn to solar wind ions as a ``tracer'' of particle trapping. On May 29, 1996, the POLAR/CAMMICE instrument observed solar wind O^6+ ions deep in the cusp, nearly 2 hours after a brief interlude of Bz southward in the midst of a strongly Bz northward solar wind stream Grande97. We then scale the 500 keV oxygen ion to a 5 keV electron (since at the same rigidity the ions and electrons follow the same trajectory, only the timescale changes), and conclude that electrons are trapped in the cusp for at least 30 minutes. Using the Bohm diffusion rate as an upper limit on stochastic acceleration, and assuming the presence of a resonant 10 mV/m cusp electric field (a typical cusp AC field as observed by POLAR/EFI) we calculate that this same 5 keV electron will cross the cusp in a few seconds, gaining ~30 keV. If it then must drift back to the top of the cusp for a second pass, that adds ~30 seconds, (see Table 1.), depending on cusp L-shell. Thirty such traversals are needed to produce an MeV, which would take approximately 15--20 minutes. Now electrostatic acceleration is most effective for lower energy electrons, whereas betatron acceleration is more effective for the higher energies, so that invoking a purely electrostatic mechanism for 1 MeV electrons may give too small an energy diffusion rate, nevertheless we appear to have sufficient time for stochastic acceleration to operate on a trapped magnetosheath population to produce radiation belt energies.

How could the cusp trap fill the dipole trap? If the cusp trap has a higher phase space density, as we show above, then diffusion into the radiation belts is allowable. The simulations show that the cusp trapping volume shrinks with increasing energy, so that above ~6 MeV, the electrons are no longer trapped. Energization processes would then cause a continual leakage of MeV particles out of the cusp. Simulations also show that some fraction, ~50\%, are lost equatorward into the pseudo-trapping region of the dipole, where they could conceivably diffuse radially inward and appear as radiation belt electrons. Other mechanisms are possible, including pitchangle scattering in the cusp itself causing the electron to exit the cusp and appear in the trapping region of the subsolar dipole trap. And as we argue in a later paper, an outward motion of the magnetopause will weaken the subsolar B-field maximum, effectively widening the ``cusp loss cone''.

Then why doesn't the cusp trap keep the outer radiation belt constantly full? Most probably because the efficiency of the mechanism has large time variations. We list several factors that control the efficiency with which the cusp can fill the outer radiation belts, which can be further classified as ``trap efficiency'' and ``accelerator efficiency.''

TABLE 1: Periods of the Motion
Energy Mu B_0 PA_0 T_0 T_1 T_2
MeV keV/nT nT degree sec sec sec
1000 16.6 26.4 41 0.004 1.0 77
1000 15.8 21.2 35 0.006 1.1 67
1000 21.5 12.8 32 0.009 0.6 28
1000 150 6.7 88 0.016 0.1 1.3
95 8.0 4.8 30 0.007 0.2 10
5 1.2 1.1 85 0.040 0.4 14


Trap Efficiency

 The volume of phase space in the trap is limited by the range of pitch angles that mirror around the cusp. The minimum pitch angle is determined by the ratio of the magnetic field strength at the cusp equator to that at the magnetopause, sin^2\alpha/sin^2\alpha_0 = |B/B_0|. Since the magnetopause Chapman-Ferraro currents are stronger near the nose, we expect the phase space volume and efficiency of the trap to increase with increasing dipole tilt. This tilt might be geometric, during the summer and winter solstices for example, or caused by dayside reconnection and erosion that tilts the cusp toward the nose.

Conversely, reconnection electric fields can distort the cusp third invariant drift orbits, causing them to move beyond the radial extent of the ``cusp equator'' and so lose their cusp second invariant. Thus a DC electric field in the cusp reduces the volume of phase space in the trap by extracting the lower energy particles, much as a DC electric field reduces the size of the plasmasphere.

The trap may also be capable of positive feedback so that sufficient trapped plasma deepens the diamagnetic cavity and enhances the trapping time, which we surmise to be the case for the May 29 or Aug 27, 1996 events Chen97. Such positive feedback can generate large variations from small perturbations such that trapping efficiencies should depend strongly on the magnetic geometry.

Accelerator Efficiency

 Stochastic acceleration is dependent upon a minimum energy ``seed population'' that can diffuse in energy space. Since in these processes, the energy gain is often proportional to the initial energy, a seed population with lower energy will take considerably longer to accelerate, perhaps longer than the trapping time. Since the trapping time can be a strong function of energy as well, this produces a sharp cutoff in the lowest energy that can be accelerated by the mechanism.

This minimum energy seed population may not always be available in the shocked magnetosheath plasma. That is, when electric fields are superposed on the cusp trap there exists a minimum energy electron above which grad_B drifts dominate over ExB and permit trapping, in complete analogy to the dipolar plasmapause. Thus slight variations in the temperature of the seed population, or in the DC electric field of cusp could result in large variations in the density of the ``seed population'' and therefore in accelerator efficiency.

Since the nightside trapped population overlap the cusp, substorm injections may also provide a seed population that must be pitchangle scattered to become trapped in the cusp. Thus the presence or absence of waves resonant with the gyrofrequency can strongly affect the seed population and accelerator efficiency.

The fluctuation power driving the acceleration mechanism may also be highly time-variable depending on reconnection rates or variations in the solar wind pressure. The 27-day recurrence of MeV electron enhancements has been tied to high speed solar wind streams, which are known to have higher fluctuation power as well. The accelerator efficiency may be non-linear in fluctuation power, since larger fluctuations may drive the chaotic and produce an Arnol'd web.

With so many degrees of freedom, it is difficult to make theoretical progress without empirical data. In a further study, we will compare several MeV electron enhancements observed at geosynchronous to this model.

Conclusions

 We have shown that the POLAR spacecraft observed trapped MeV electrons in the Earth's cusp, and that these distributions are consistent with particles trapped in the outer cusp simulated using the Tsyganenko 96 model. Although this trapping geometry is quite different than the standard dipole geometry, we show that an analogous three invariants of the motion exist for this trapped population as well. We show that trapping alone or electric fields alone are not sufficient to produce an energetic electron enhancement, but in concert may be very effective at accelerating electrons to MeV energies. Thus the efficiency of the acceleration mechanism can be highly time variable, producing a typical 2-day time delayed response with respect to the arrival of a high speed solar wind stream, or an 8 hour response as observed on January 10, 1997, or even no response at all Blake97. If cusp trapping and energization could be established as the origin of the 1-10 MeV outer radiation belt ``killer'' electrons and as the explanation for the variable efficiency of the solar wind drivers, it would be a major breakthrough in space weather and permit the specification and prediction of a major natural hazard to Earth orbiting satellites.

Acknowledgements

 This study was supported by NASA contract NAS5-97147. We gratefully acknowledge the POLAR/CEPPAD data provided by B. Blake and the magnetic field data provided by C. Russell.

References

TOC Comments? r*bs@rbsp.info
(due to spamming, delete the asterisk)