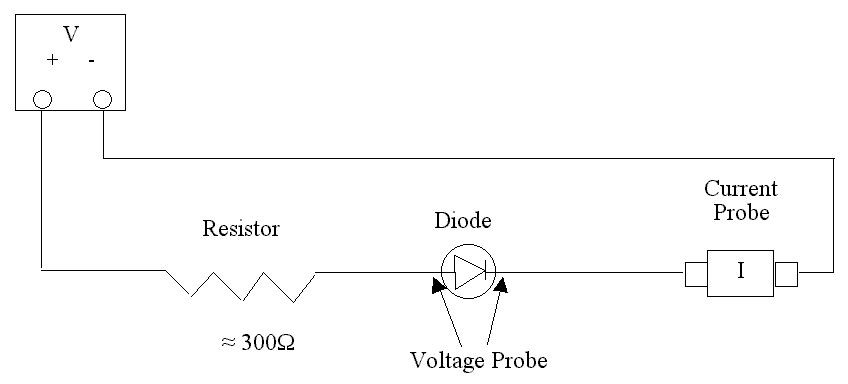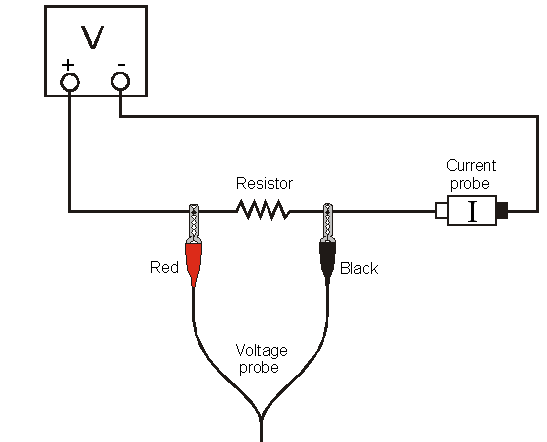
Figure 1
| Electrical Quantity | Description | Units | Water Analogy |
| Voltage or Potential Difference |
A measure of the Energy difference per unit charge between two points in a circuit. |
Volts (V) | Water Pressure |
| Current | A measure of the flow of charge in a circuit. |
Amperes (A) | Amount of water flowing |
| Resistance | A measure of how difficult it is for current to flow in a circuit. |
Ohms (Ω) | A measure of how difficult it is for water to flow in a pipe. |

| Power Macintosh | wires |
| Lab Pro | clips to hold wires |
| Logger Pro 2.1 | light bulb (6.3 V) |
| Adjustable 5-volt DC power supply | two resistors (about 10 and 50 Ω) |
| Vernier Current & Voltage Probe System |
| Slope of regression line (V/A) |
Y-intercept of regression line (V) |
|
| Resistor Ω | ||
| Resistor Ω | ||
| Light bulb (first 3 pts) | ||
| Light bulb (last 10 pts) |