Electrical Potential

Recall the expression of the Coulomb force exerted on charge 1 by charge 2, as given in the figure, is:

where k is a constant that equals 9.0 X 10⁹ N m²/C².

Charles Coulomb did his experimental investigations of this force in the 18th century by exploring the forces between two small charged spheres. Much later, in the 20th century Coulomb's law enabled scientist to design cyclotrons and other types of accelerators for moving charged particles in circular orbits at high speeds.

Newton's discovery of the universal law of gravitation came the other way around. He thought about orbits first. This was back in the 17th century long, before Coulomb began his studies. A statement of Newton's universal law of gravitation describing the force experienced by mass 1 due to the presence of mass 2 is shown below in modern mathematical notation:

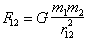
where G is equal to 6.67 x 10^-11 Nm²/Kg².

About the time that Coulomb did his experiments with electrical charges in the 18th century, one of his contemporaries, Henry Cavendish, did a direct experiment to determine the nature of the force between two spherical masses in a laboratory. This confirmed Newton's gravitational force law and allowed him to determine the gravitational constant G.

Recall that the work required to move an object in the Earth's gravitational field is path independent. We therefore refer to the gravitational force as a conservative force, and can define a change in the potential energy of an object relative to another by negative the work required to move the object. In a region where the force of gravity is approximately a constant (such as near the surface of the Earth), the change in potential energy is proportional to a change in height. The following plots give us several graphical views of the same data--the Maroon Bells quad in the Coloroda Rockies. Note how altitude can be displayed as contour lines (panel 1, a contour map), or a perspective (panel 2, a surface plot) or color (panel 3, a color contour plot), or all 3 (panel 4).

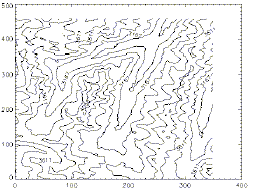
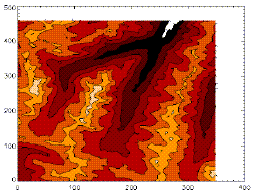
This gives us a useful picture for potential energy. Consider a contour map. Each line of constant height in the contour map is also a line of constant gravitational potential energy. Also, consider the net force on an object sitting on the surface defined by the contour map. It will be down any hill, and perpendicular to the line of constant height.

Since the electrostatic force has the same mathematical form as the gravitational force, we can make similar definitions. Consider the force on a small positive charge (call it q₀) from some set of charges. If q₀ is moved then these charges will do work on q₀. Since the electrostatic force is also a conservative force, we can say that there is a change in potential energy when we move the small charge, where 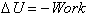. If we don't want our picture of the electrostatic "landscape" to depend on the size of our test charge q₀, we can define the change in the Electric Potential as the potential energy per unit charge, or .

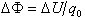OBJECTIVES

• To map and examine the potential distribution in two dimensions for several simple sets of electrodes.
• To learn how to determine electric field lines from equipotential surfaces and vice versa.
• To become familiar with the use of a multimeter.

MATERIALS

• Field Mapper kit (cork board, conductive paper, metal tacks and wires)
• LabPro with probes
• Battery packs or power supply
• Extra wires and switches
• Paper overlay sheets for drawing results

PROCEDURE

Part I Mapping the Potential

1. You are given two sheets of conductive paper on which patterns have already been drawn with conductive ink. Select one of the sheets (either the parallel lines or the two "point" charges). You will return and complete the lab for the other pattern later. The most common source of problems in this lab is with the conductive lines. The ink can crack causing breaks in the conductive lines, or the tacks can fail to make good contact with the ink. If your setup looks suspicious, notify your instructor or TA!
2. You will use the voltage inputs of the LabPro or the probes of a multimeter to measure the potential difference. ( To use the LabPro start you computer and open Logger Pro and open a new meter window showing only potential. Select live inputs) . Since volts are the SI units of electric potential potential difference is often called Voltag). The ULI measures the difference in electric potential between its inputs. You connect two probes to the inputs. Since the probes and their connecting wires are good conductors (at least compared to the black paper), there is little electric field in the wires, and so little change in potential from the probe tip to the meter. There are two sets of probes connected to the ULI. Use the set that is not taped together for the first part of this lab.
3. Like potential energy, electric potential is defined as a difference. Therefore, one can always set an arbitrary zero point for the potential. For the purposes of this lab, we will define the zero potential point to be the negative terminal of the power supply.
4. Set up the circuit as shown above. The battery pack should read near 5 volts. Use the alligator clips to connect the terminals of the battery to each of the electrodes (metal tacks) on the paper.
5. Connect the probes from the multimeter to the two electrodes. This should give very close to the same reading as the potential difference between the two terminals of the power supply itself. If not, there may be some bad connection. Try to correct this yourself before calling for the instructor or TA. Adjust the multimeter range to the smallest range that will read this potential difference.
6. You are to plot out equipotential lines on each of the two patterns. (Once you have completed both parts I and II for one sheet, return and complete both sections for the other). Equipotentials are plotted by connecting one lead of the voltmeter (the ground or common, by convention this is often the black lead) to the electrode connected to the negative battery terminal. The other voltmeter lead (the probe) is used to measure the potential at any point on the paper by simply touching the probe to the paper at that point.
7. To map an equipotential, move the probe until the desired potential is indicated on the multimeter. You are to mark this point on the sheets provided (these sheets have the same grid markings as on the conductive paper). Continue to move the probe, but only in a direction that maintains the meter at the same reading. Continue to mark these points. Connecting the points produces an equipotential line.
8. Draw at least eight equipotential lines, for equal steps in potential difference. For potentials that are close to zero or the full battery potential, this may be difficult and may take some care.

Part II Mapping the field lines

1. To plot the field lines, neither lead of the voltmeter is connected to an electrode. Instead, the two leads of the multimeter will be placed on the conductive paper side by side at a set distance. (It may help to tape the two leads together for this procedure--this should have been done for you already with the other set of leads.) The technique is to use the multimeter leads to find the direction that follows the path of greatest potential difference from point to point
2. Just as the net force on an object resting on a hill is in the direction of the steepest slope, so the electric field at any point is in the direction of greatest change in the potential. (In fact, the magnitude of the field is given by 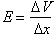) To find this direction, place the ground multimeter probe on the paper near one of the terminals. Place the other multimeter lead on the paper and note the multimeter reading. Now pivot the lead to several positions while keeping the ground lead stationary. Note the multimeter readings as you touch the lead at each new spot. (Do not drag the leads). When the potential difference is the highest, draw an arrow from the high potential spot, back to the position of the ground lead. (Remember that the force is downhill.) You may need to increase the sensitivity of your multimeter for this section.
3. Move the ground lead to the former position of the other lead and repeat the action of pivoting and touching with the front lead until the potential reading is the highest. Draw the next arrow. Repeat this action across the paper. Eventually, the arrows will form a field line.
4. Return to the original terminal, select a new point near the terminal and plot another field line. For the "point charges" select several positions around one of the points. For the parallel lines pattern, choose several positions about the line. Be sure to pick some near the center of the line, some near the edge, and some positions in between. Draw at least 4 field lines on each.
5. Return and complete sections I and II for the other sheet.

DATA

ANALYSIS

1. In general, you should be able to note two relations between the equipotentials and the field (one observation for the direction, one for the field strength). What are these relations?

2. For the parallel lines, what is the nature of the field inside the lines? How does the potential change? What is the field outside the lines? How are the field lines related to the conducting lines themselves?

3. For the "point charges": Where is the field the strongest? What path could a small positive charge follow from "infinitely" far away to get to a point between the charges without doing any work?

EXTENSIONS

1. Draw several parallel line configurations, with the same length of line, but different spacing between the lines. How does this effect the strength of the field inside the lines? How does it effect the fringing of the field outside the lines?
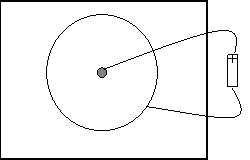2. Point source and guard ring:
   What relation can you determine between the distance from the center of the point source and the potential value? What about the field strength? (You may need to play around with the data in Graphical Analysis.)
   
3. Ask your instructor for other ideas to investigate: Point charges of like sign, field near a sharp point, floating conductors or floating insulators. In each of these cases, you are looking for relationships between the equipotentials, the field lines, and the shapes of the conducting (or insulating) regions.