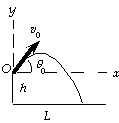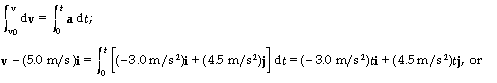Chapter 3

Homework Problems

Solutions

(a) For the components we have
	Rx	= Bx - 2Ax 
		= - 26.5 cos 56.0° - 2(44.0 cos 28.0° ) 
		= - 92.5;
	Ry	= By - 2Ay 
		= 26.5 sin 56.0° - 2(44.0 sin 28.0°) 
		= - 19.3.
  We find the resultant from
	R 	= (Rx^2 + Ry^2)^1/2 = [(- 92.5)^2 + (- 19.3)^2]^1/2 
		=         94.5;
	tan theta= Ry/Rx = (19.3)/(92.5) = 0.209, which gives         
	theta = 11.8° below - x-axis.
(b) For the components we have
	Rx	= 2Ax - 3Bx + 2Cx 
		= 2(44.0 cos 28.0°) - 3(- 26.5 cos 56.0°) + 2(0) 
		= 122.2;
	Ry	= 2Ay - 3By + 2Cy
		= 2(44.0 sin 28.0° ) - 3(26.5 sin 56.0°) + 2(- 31.0) 
		= - 86.6.
  We find the resultant from
	R 	= (Rx2 + Ry2)1/2 = [(122.2)2 + (- 86.6)2]1/2 
		=         150;
      tan theta = Ry/Rx = (86.6)/(122.2) = 0.709, which gives         
	  theta = 35.3° below + x-axis.

(a) For the vertical component we have
	aV = (3.80 m/s^2) sin 30.0° =        1.90 m/s^2 down.
(b) Because the elevation change is the vertical displacement, 
we find the time from the 
vertical motion, taking down as the positive direction:
	y = v0y t + 1/2 aV t^2;
	250 m = 0 + 1/2 (1.90 m/s^2)t^2, which gives          t = 16.2 s.

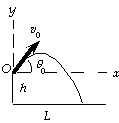
(a) We choose a coordinate system with the origin at the jump point, 
	with x horizontal and y vertical, with the positive direction up. 
	The horizontal motion will have constant velocity:
	x = x0 + v0x t; 
	L = 0 + v0 cos theta_0 t;
	3.0 m =  (v0 cos theta_0)(1.3 s), which gives v0 cos theta_0 = 2.31 m/s.
  For the vertical motion we have
	y = y0 + v0y t + 1/2ay t^2;  
	- h = 0 + (v0 sin theta0)t + 1/2(- g)t2;
	- 5.0 m = (v0 sin theta0)(1.3 s) - 1/2(9.80 m/s2)(1.3 s)^2, 
	which gives v0 sin theta0 = 2.52 m/s.
  When we divide the two equations, we get
	tan theta0= 1.093,  theta0 = 47.5°.
  Thus we find the magnitude of v0 from
	v0 sin 47.5° = 2.52 m/s, which gives v0 = 3.42 m/s, so
	v0 =  3.42 m/s, 47.5° above the horizontal.
(b) At the maximum height the vertical velocity will be zero.  
    We find the maximum height from
	vy^2 = v0y^2 + 2a y;
	0 = (v0 sin theta0)^2 + 2(- g)hmax ; 
	hmax = v0^2 sin 2 theta0/2g = (3.42 m/s)^2 sin2 (47.5°)/2(9.80 m/s^2) 
	= 0.32 m,  or     5.32 m above the water.
(c) The horizontal velocity is constant.  We find the vertical velocity from
	vfy^2 = v0y^2 + 2a y;
	vfy^2 = (3.42 m/s)^2 sin 2 (47.5°) - 2(9.80 m/s^2)(- 5.0 m), 
  which gives vfy = - 10.2 m/s.
  We find the direction from
	tan theta = vfy/vfx = (- 10.2 m/s)/(2.31 m/s) = - 4.42, 
  which gives        
	theta = 77° below the horizontal.
  We find the magnitude of v from
	vf sin 77° = 10.2 m/s, which gives vf = 10.5 m/s, so
	vf =  10.5 m/s, 77° below the horizontal.

 To complete an orbit in time T, the speed of the shuttle must be
	v= 2pi r/T.
  Thus the centripetal acceleration in terms of g is 
	a_R/g = v^2/rg = (2pi r/T)^2/rg = 4pi^2r/gT^2 
	= 4pi^2(6.38x10^6 m + 0.40x10^6 m)/(9.80 m/s^2)[(90 min)(60 s/min)]^2,
	 which gives 
	      a_R = 0.94g.

If v_PW is the velocity of the passenger with respect to the water, 
   v_PB the velocity of the passenger with respect to the boat, and 
   v_BW the velocity of the boat with respect to the water, then 
   v_PW = v_PB + v_BW , as shown in the diagram. 
  From the diagram we find the two components of v_PW:
	v_PWx	= v_PB cos 45° + v_BW 
		= (0.60 m/s) cos 45° + 1.80 m/s = 2.22 m/s.
	v_PWy	= v_PB sin 45° = (0.60 m/s) sin 45° = 0.424 m/s.
  For the magnitude we have
	v_PW = (v_PWx^2 + v_PWy^2)^1/2 = [(2.22 m/s)^2 + (0.424 m/s)^2]^1/2 =        2.26 m/s.
We find the angle from
	tan theta = v_PWy/v_PWx = (0.424 m/s)/(2.22 m/s) = 0.191, 
  which gives        
	theta = 11° above the water.

If v_AG is the velocity of the automobile with respect to the ground, 
   v_HG the velocity of the helicopter with respect to the ground, and 
   v_HA the velocity of the helicopter with respect to the automobile,
 then
   v_HA = v_HG - v_AG .
 For the horizontal relative velocity we have  
   v_HA = v_HG - v_AG = (200 km/h - 150 km/h)/(3.6 ks/h) = 13.9 m/s.
 This is the initial (horizontal) velocity of the parcel, so we can find the
 time of fall from
	y = y0 + v0yt + 1/2ay t^2;    
	78.0 m = 0 + 0 + 1/2(+ 9.80 m/s2)t^2, which gives t = 3.99 s.
 During this time, we find the horizontal distance the parcel travels with
 respect to the car from
	x = v_HA t = (13.9 m/s)(3.99 s) = 55.4 m.
 Because the helicopter is always directly above the parcel, this is how far 
 behind the automobile the helicopter must be when the parcel is dropped. 
 Thus we find the angle from
	tan theta = y/x = (78.0 m)/(55.4 m) = 1.41, 
  which gives       
        theta = 54.6° below the horizontal.

	

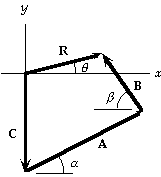
(a) For the components we have	
	Rx	= Ax + Bx + Cx 
		= 44.0 cos 28.0° - 26.5 cos 56.0° + 0 =        24.0;
	Ry	= Ay + By + Cy
		= 44.0 sin 28.0° + 26.5 sin 56.0° - 31.0 =        11.6.
(b) We find the resultant from
	R = (Rx^2 + Ry^2)^1/2 = [(24.0)^2 + (11.6)^2]^1/2  =         26.7;
	tan theta = Ry/Rx = (11.6)/(24.0) = 0.483, which gives         
	theta = 25.8° above + x-axis. 
	

 The acceleration is a = (- 3.0 m/s^2)i + (4.5 m/s^2)j.
 We find the velocity by integrating:

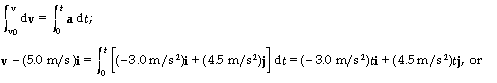
	v = [(- 3.0 m/s^2)t + 5.0 m/s]i + [(4.5 m/s^2)t]j.
 We find the position by integrating:

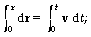
To find the time at which the particle reaches its maximum x-coordinate, 
we set dx/dt = 0:
	dx/dt = (- 3.0 m/s^2)t + 5.0 m/s = 0, which gives t = 1.67 s.
The velocity is
	v = [(- 3.0 m/s^2)t + 5.0 m/s]i + [(4.5 m/s^2)t]j 
	  = 0i + (4.5 m/s^2)(1.67 s)j =      (7.5 m/s)j.
The position is
  r   = [(- 1.5 m/s^2)t^2 + (5.0 m/s)t]i + (2.25 m/s^2)t^2 j 
      = [(- 1.5 m/s^2)(1.67 s)^2 + (5.0 m/s)(1.67 s)]i + (2.25 m/s^2) (1.67 s)^2j 
      =       (4.2 m)i + (6.3 m)j.

      

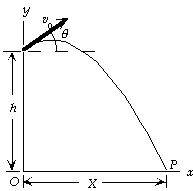
(a) We choose a coordinate system with the origin at the 
  base of the cliff, with x horizontal and y vertical, with 
  the positive direction up.   We find the time required for 
  the fall from the vertical motion:
	y = y0 + v0y t + 1/2 ay t^2;  
	0 = 125 m + (65.0 m/s)(sin 37.0°)t + 1/2(- 9.80 m/s^2)t^2, 
  which gives t = - 2.45, 10.4 s.
  Because the projectile starts at t = 0, we have           t = 10.4 s.
(b) We find the range from the horizontal motion:
	X 	= v0x t = (65.0  m/s)(cos 37.0°)(10.4 s) 
		=        540 m .
(c)  For the velocity components, we have
	vx = v0x = (65.0  m/s) cos 37.0° =         51.9 m/s.
	vy = v0y + ay t = (65.0  m/s) sin 37.0° + (- 9.80 m/s^2)(10.4 s) 
	  =         - 62.8 m/s.
(d) When we combine these components, we get
	v = (vx^2 + vy^2)^1/2 = [(51.9 m/s)^2 + (- 62.8 m/s)^2]^1/2 
	=         81.5 m/s.
(e) We find the angle from
	tan theta = vy/vx = (62.8 m/s)/(51.9 m/s) = 1.21,
 which gives
        theta = 50.4° below the horizontal.

 An object at the equator is moving with the rotational speed 
of the surface of the Earth:
	v = 2pi r_E/T = 2pi(6.38x10^6 m)/(86,400 s) = 464 m/s.
  The acceleration of gravity is reduced by the radial acceleration:
  Thus 
        -g = - v^2/r_E =  - (464 m/s)^2/(6.38x10^6 m) 
	   =        - 0.0337 m/s2 (0.343% of g).

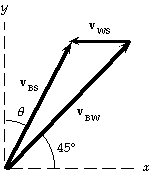
If v_BS is the velocity of the boat with respect to the shore, 
   v_BW the velocity of the boat with respect to the water, and 
   v_WS the velocity of the water with respect to the shore, then 
   v_BS = v_BW + v_WS , as shown in the diagram. 
  We find the angle of the boat's motion with respect to the shore 
  from the distances:
	tan theta = d_shore/d_river = (120 m)/(280 m) = 0.429, 
  which gives theta = 23.2°.
  The y-component of v_BS is also the y-component of v_BW:
	v_BSy = v_BWy  = (2.40 m/s) sin 45° = 1.70 m/s.
  We find the x-component from
	v_BSx = v_BSy tan theta  = (1.70 m/s) tan 23.2° = 0.727 m/s.
  For the x-component of the relative velocity, we use the diagram to get
	|v_WS| = v_BWx - v_BSx = (2.40 m/s) cos 45° - 0.727 m/s =        0.97 m/s.
	

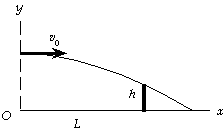
  We use the coordinate system shown in the diagram.
  We find the time for the ball to reach the net from the 
  vertical motion:
	y = y0 + v0y t + 1/2ay t^2;    
	0.90 m = 2.50 m + 0 + 1/2(- 9.80 m/s^2)t^2, which gives t = 0.571 s.
  We find the initial velocity from the horizontal motion:
	x = v0x t;    
	15.0 m = v0 (0.571 s), which gives  v0 = 26.3 m/s.  
  We find the time for the ball to reach the ground from the 
  vertical motion:
	y = y0 + v0y t2 + 1/2ay t2^2;    
	0 = 2.50 m + 0 + 1/2(- 9.80 m/s^2)t2^2, which gives         t2 = 0.714 s.
  We find where it lands from the horizontal motion:
	x2 = v0 t2 = (26.3 m/s)(0.714 s) = 18.8 m.  
  Because this is 18.8 m - 15.0 m =       3.8 m beyond the net,
  which is less than 7.0 m, the serve is       good.
  

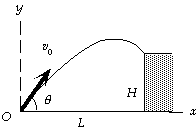
  We use the coordinate system shown in the diagram, 
  with up positive.  For the horizontal motion, we have
	x = v0x t;    
	L = (v0 cos theta)t;
	195 m = (v0 cos theta)(7.6 s), which gives v0 cos theta = 25.7 m/s.
  For the vertical motion, we have
	y = y0 + v0y t + 1/2ay t^2; 
	H = 0 + (v0 sin theta)t + 1/2(- g)t^2;
	155 m = (v0 sin theta)(7.6 s) + 1/2(- 9.80 m/s^2)(7.6 s)^2, 
  which gives v0 sin theta = 57.6 m/s.
  We can find the initial angle theta by dividing the two results:
	tan theta = (v0 sin theta )/(v0 cos theta ) 
	          = (57.6 m/s)/(25.7 m/s) = 2.24, which gives  theta = 66.0°.
  Now we can use one of the previous results to find the initial velocity:
	v0 = (25.7 m/s)/cos theta  = (25.7 m/s)/cos 66.0° = 63 m/s.
  Thus the initial velocity is        63 m/s, 66° above the horizontal.