Chapter 4 Solutions
23,35,41,46,67,75; 25,32,40,50,68,73; 53,55

23. We find the velocity necessary for the jump from the motion when the
person leaves the ground to the highest point, where the velocity is zero:
v^2 = vjump^2 + 2(- g)h;
0 = vjump^2 + 2(- 9.80 m/s^2)(0.80 m), which gives vjump = 3.96 m/s.
We can find the acceleration required to achieve this velocity during the
crouch from
vjump^2 = v0^2 + 2a(y - y0);
(3.96 m/s)^2 = 0 + 2a(0.20 m - 0), which gives a = 39.2 m/s^2.
Using the force diagram for the person during the crouch, we can write Sum(F) = ma:
FN - mg = ma;
FN - (61 kg)(9.80 m/s^2) = (61 kg)(39.2 m/s^2), which gives FN = 3.0 x 10^3 N.
From Newton?s third law, the person will exert an equal and opposite force on the ground:
3.0 x 10^3 N downward.
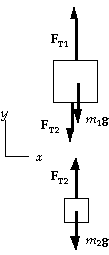
35. (a) Because the buckets are at rest, the acceleration is zero.
We write Sum(F) = ma from the force diagram for each bucket:
lower bucket: FT2 - m2 g = m2 a = 0, which gives
FT2 = m2 g = (3.5 kg)(9.80 m/s^2) = 34 N.
upper bucket: FT1 - FT2 - m1 g = m1 a = 0, which gives
FT1 = FT2 + m1 g = 34 N + (3.5 kg)(9.80 m/s^2) = 68 N.
(b) The two buckets must have the same acceleration.
We write Sum(F) = ma from the force diagram for each bucket:
lower bucket: FT2 - m2 g = m2 a, which gives
FT2 = m2(g + a)
= (3.5 kg)(9.80 m/s^2 + 1.60 m/s^2) = 40 N.
upper bucket: FT1 - FT2 - m1g = m1a, which gives
FT1 = FT2 + m1(g + a)
= 40 N + (3.5 kg)(9.80 m/s^2 + 1.60 m/s^2) = 80 N.
Note that we could have taken both buckets as the
system to find the tension in the upper cord.
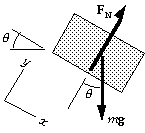
41. We choose the origin for x at the bottom of the plane.
Note that down the plane (the direction of the acceleration) is positive.
(a) From the force diagram for the block, we have Sum(F) = ma:
x-component: mg sin q = m a;
y-component: FN - mg cos q = 0.
From the x-equation we find the acceleration:
a = g sin q = (9.80 m/s^2) sin 22deg = 3.67 m/s^2.
For the motion of the block, we find the distance until it
momentarily stops from
v^2 = v0^2 + 2a(x - x0);
0 = (- 4.0 m/s)^2 + 2(3.67 m/s^2)(x - 0), which gives x = - 2.2 m.
Thus the block travels 2.2 m up the plane.
(b) We find the time from the start to return to the bottom from
x = x0 + v0 t + 1/2a t^2;
0 = 0 + (- 4.0 m/s)t + 1/2(3.67 m/s^2)t^2,
which gives t = 0 (the start), and t = 2.2 s.
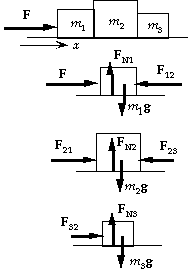
46. (a)
(b) If we select all three blocks as the system, we have
Sum(Fx) = m ax: F = (m1 + m2 + m3)a,
which gives a = F/(m1 + m2 + m3).
(c) For the three blocks individually, for Sum(Fx) = m ax, we have
Fnet1 = m1 a = m1 F/(m1 + m2 + m3);
Fnet2 = m2 a = m2 F/(m1 + m2 + m3);
Fnet3 = m3 a = m3 F/(m1 + m2 + m3).
(d) From the force diagram for block 1 we have
Fnet1 = F - F12 = m1 a, which gives
F12 = F - m1 a = F - m1 F/(m1 + m2 + m3)
= F(m2 + m3)/(m1 + m2 + m3).
This is also F21 (Newton's third law).
From the force diagram for block 2 we have
Fnet2 = F21 - F23 = m2a, which gives
F23 = F21 - m2 a = F - m1a - m2a
= F - (m1 + m2)F/(m1 + m2 + m3)
= F m3/(m1 + m2 + m3).
This is also F32 (Newton's third law).
(e) When we use the given values, we get
a = F/(m1 + m2 + m3) = (96.0 N)/(12.0 kg + 12.0 kg + 12.0 kg) = 2.67 m/s2.
Fnet1 = m1 a = (12.0 kg)(2.67 m/s^2) = 32.0 N.
Fnet2 = m2 a = (12.0 kg)(2.67 m/s^2) = 32.0 N.
Fnet3 = m3 a = (12.0 kg)(2.67 m/s^2) = 32.0 N.
Because the blocks have the same mass and the same acceleration, we expect
Fnet1 = Fnet2 = Fnet3 = 32.0 N.
For the forces between the blocks we have
F21 = F12 = F - m1 a
= 96.0 N - (12.0 kg)(2.67 m/s^2) = 64.0 N.
F32 = F23 = F - m1 a - m2a
= 96.0 N - (12.0 kg)(2.67 m/s^2) - (12.0 kg)(2.67 m/s2) = 32.0 N.
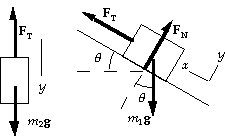
67. (a) The forces and coordinate systems are shown in the
diagram. Note that we take up the incline as the
positive direction. From the force diagram, with
the block m2 as the system, we can write Sum(F) = m a:
y-component: m2 g - FT = m2 a.
From the force diagram, with the block m1 as the system,
we can write Sum(F) = m a:
x-component: FT - m1 g sin q = m1 a.
When we eliminate FT between these two equations, we get
a = (m2 - m1 sin q)g/(m1 + m2).
= [1.00 kg - (1.00 kg)(sin 30deg)](9.80 m/s^2)/(1.00 kg + 1.00 kg)
= 2.45 m/s^2 (up the incline).
(b) If the system remains at rest, the acceleration is zero, so we have
a = (m2 - m1 sin q)g/(m1 + m2) = 0, or
m2 = m1 sin q = (1.00 kg)(sin 30deg) = 0.50 kg.
(c) From the force equations, we have
FT = m2(g - a).
For part (a), we get
FT = (1.00 kg)(9.80 m/s^2 - 2.45 m/s^2) = 7.35 N.
For part (b), we get
FT = (0.50 kg)(9.80 m/s^2 - 0) = 4.9 N.
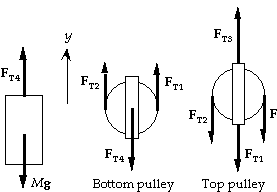
75. There are only three different tensions. The tension
in the rope that goes around both pulleys is constant:
FT1 = FT2 = F.
We choose up positive and assume that the piano
is lifted with no acceleration.
If the masses of the pulleys are negligible,
we can write Sum(Fy) = m ay.
(a) If we select the piano and bottom pulley as
the system, we have
FT2 + FT1 - Mg = 0, which gives
2 FT1 = Mg, or FT1 = F = 1/2 Mg.
(b) For the individual elements, we have
piano: FT4 - Mg = 0, which gives
FT4 = Mg.
bottom pulley: FT2 + FT1 - FT4 = 0, which gives
2FT1 = FT4 = Mg, or FT1 = FT2 = 1/2 Mg.
top pulley: FT3 - FT1 - FT2 - F = 0, which gives
FT3 = 3FT1 = 1/3 Mg.

25. (a) If we assume that he accelerates for a time t1 over
the first 45 m and reaches a top speed of v, we have
x1 = 1/2(v0 + v)t1 = 1/2v t1 , or t1 = 2 x1/v = 2(45 m)/v = (90 m)/v.
Because he maintains this top speed for the last 55 m, we have
t2 = (55 m)/v.
Thus the total time is T = t1 + t2 = (90 m)/v+ (55 m)/v = 10.0 s.
When we solve for v, we get v = 14.5 m/s; so the acceleration time is
t1 = (90 m)/(14.5 m/s) = 6.21 s.
We find the constant acceleration for the first 45 m from
a = v/t = (14.5 m/s - 0)/(6.21 s) = 2.34 m/s^2.
We find the horizontal force component that will produce this acceleration from
F = ma = (62 kg)(2.34 m/s^2) = 1.4 x 10^2 N.
(b) As we found in part (a): v = 14.5 m/s.
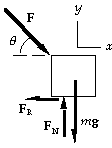
32. (a)
(b) Because the velocity is constant, the acceleration is zero.
We write Sum(F) = ma from the force diagram for the mower:
x-component: F cos q - FR = ma = 0, which gives
FR = (78.0 N) cos 45deg = 55.2 N.
(c) y-component: FN - mg - F sin q = ma = 0, which gives
FN = (13.0 kg)(9.80 m/s^2) + (78.0 N) sin 45deg = 183 N.
(d) We can find the acceleration from the motion of the mower:
a = v/t = (1.2 m/s - 0)/(2.0 s) = 0.60 m/s^2.
For the x-component of Sum(F) = ma we now have
F cos q - FR = ma;
F cos 45deg - 55.2 N = (13.0 kg)(0.60 m/s^2), which gives F = 89 N.
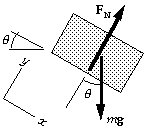
40. (a) From the force diagram for the block, we have Sum(F) = ma:
x-component: mg sin q = ma;
y-component: FN - mg cos q = 0.
From the x-equation we find the acceleration:
a = g sin q = (9.80 m/s^2) sin 22.0deg = 3.67 m/s^2.
(b) For the motion of the block, we find the speed from
v^2 = v0^2 + 2a(x - x0);
v^2 = 0 + 2(3.67 m/s^2)(12.0 m - 0), which gives v = 9.39 m/s.

50. Forces are drawn for each of the blocks. Because the string
doesn't stretch, the tension is the same at each end of the
string, and the accelerations of the blocks have the same
magnitude. Note that we take the positive direction in the
direction of the acceleration for each block.
We write Sum(F) = ma from the force diagram for each block:
y-component (block 1): FT - m1 g = m1 a;
y-component (block 2): m2 g - FT = m2 a.
By adding the equations, we find the acceleration:
a = (m2 - m1)g/(m1 + m2)
= (3.2 kg - 2.2 kg)(9.80 m/s^2)/(3.2 kg + 2.2 kg)
= 1.81 m/s^2 for both blocks.
For the motion of block 1 we take the origin at the ground
and up positive. When block 2 hits the ground, we have
v1^2 = v01^2 + 2a(y1 - y01)
= 0 + 2(1.81 m/s^2) (3.60 m - 1.80 m), which gives
v1 = 2.56 m/s.
Once block 2 hits the ground, FT Æ 0 and block 1 will have the downward acceleration of g.
For this motion of block 1 up to the highest point reached, we have
v^2 = v1^2 + 2a(h - y1)
0 = (2.56 m/s)^2 + 2(- 9.80 m/s^2) (h - 3.60 m), which gives h = 3.93 m.
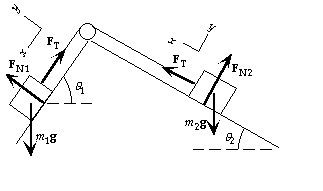
68. (a) Forces are drawn for each of the blocks.
Note that we use two different coordinate
systems. We write Sum(F) = ma from the
force diagram for each block:
For block 1:
x-component: m1 g sin q1 - FT = m1a.
For block 2:
x-component: FT - m2 g sin q2 = m2 a.
By adding the equations, we have
a = (m1 sin q1 - m2 sin q2)g/(m1 + m2).
(b) If the system remains at rest, the
acceleration is zero, so we have
a = (m1 sin q1 - m2 sin q2)g/(m1 + m2) = 0, or
m1 sin q1 = m2 sin q2;
(5.0 kg)(sin 30deg) = m2 sin 20deg, which gives m2 = 7.3 kg.
From the force equations, we have
FT = m1(g sin q1 - a) = (5.0 kg)[(9.80 m/s^2 )(sin 30deg) - 0] = 25 N.
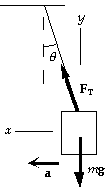
73. From the force diagram for the watch, we have Sum(F) = ma:
x-component: FT sin q = ma;
y-component: FT cos q - mg = 0, or FT cos q = mg.
If we divide the two equations, we find the acceleration:
a = g tan q = (9.80 m/s^2) tan 25deg = 4.56 m/s^2.
For the motion of the aircraft, we find the takeoff speed from
v = v0 + at = 0 + (4.56 m/s^2)(18 s) = 82 m/s (300 km/h).
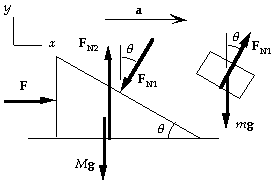
53. If m does not move on the incline, both blocks must have
the same horizontal acceleration. From the force
diagram for the block of mass m, we have Sum(F) = ma:
x-component: FN1 sin q = ma;
y-component: FN1 cos q - mg = 0.
When we combine these two equations, we get:
a = g tan q, and FN1 = mg/cos q.
From the force diagram for the block of mass M, we
have Sum(F) = ma:
x-component: F - FN1 sin q = Ma;
y-component: FN2 -FN1 cos q - Mg = 0.
We use the previous results in the first equation to get
F = mg tan q + Mg tan q = (m + M)g tan q.
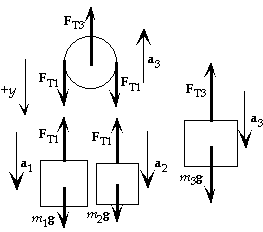
55. The force diagrams for each of the masses and the movable pulley are shown.
Note that we take down as positive and the indicated accelerations are
relative to the fixed pulley. A downward acceleration of m3 means an
upward acceleration of the movable pulley. If we call ar the (downward)
acceleration of m1 with respect to the movable pulley, we have
a1 = ar - a3 and a2 = - ar - a3 ,
because the acceleration of m2 with respect to the pulley
must be the negative of m1?s acceleration with respect to
the pulley. If the mass of the pulley is negligible, for
the movable pulley we write Sum(Fy) = m ay:
2FT1 - FT3 = (0)(- a3), so 2FT1 = FT3.
For each of the masses, for Sum(Fy) = m ay we get
mass m1: m1 g - FT1 = m1 a1 = m1(ar - a3),
mass m2: m2 g - FT1 = m2 a2 = m2(- ar - a3),
mass m3: m3 g - FT3 = m3 a3.
We have four equations for the four unknowns:
FT1 , FT3 , ar , and a3.
After some careful algebra, we get
a3 = [(m1 m3 + m2 m3 - 4m1 m2)/(m1 m3 + m2 m3 + 4m1 m2)]g;
ar = [2(m1 m3 - m2 m3)/(m1 m3 + m2 m3 + 4m1 m2)]g;
FT1 = [4m1 m2 m3/(m1 m3 + m2 m3 + 4m1 m2)]g; and
FT3 = [8m1 m2 m3/(m1 m3 + m2 m3 + 4m1 m2)]g.
We can now find the other accelerations:
a1 = [(m1 m3 ? 3m2 m3 + 4m1 m2)/(m1 m3 + m2 m3 + 4m1 m2)]g;
a2 = [(- 3m1 m3 + m2 m3 + 4m1 m2)/(m1 m3 + m2 m3 + 4m1 m2)]g.













