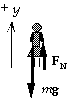Chapter 6 Solutions
Problems: 6: 7,9,23,33,37,57;8,11,25,45,60,62;17
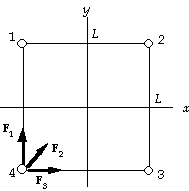
7. We choose the coordinate system shown in the figure and
find the force on the mass in the lower left corner.
Because the masses are equal, for the magnitudes of the
forces from the other corners we have
F1 = F3 = Gmm/r12
= (6.67x10-11 N · m2/kg2)(8.5 kg)(8.5 kg)/(0.70 m)2
= 9.83x10-9 N;
F2 = Gmm/r22
= (6.67x10-11 N · m2/kg2)(8.5 kg)(8.5 kg)/[(0.70 m)/cos q45°]2
= 4.92x10-9 N.
From the symmetry of the forces we see that the resultant will be
along the diagonal. The resultant force is
F = 2F1 cos q=45° + F2
= 2(9.83x10-9 N) cos q=45° + 4.92x10-9 N
= 1.9x10-8 N toward center of the square.
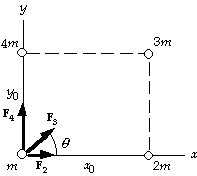
9. For the magnitudes of the forces on the mass m from the other
masses we have
F2 = Gm(2m)/x02 = 2Gm2/x02;
F3 = Gm(3m)/(x02 + y02) = 3Gm2/(x02 + y02);
F4 = Gm(4m)/y02 = 4Gm2/y02.
The force F3 is at an angleq above the x-axis, with
sin q = y0/(x02 + y02)1/2, and cos q = x0/(x02 + y02)1/2.
Thus the resultant force is
F = (F2 + F3 cos q)i + (F3 sin q + F4)j
= Gm2{(2/x02) +[3/(x02 + y02)][x0/(x02 + y02)1/2]}i +
Gm2{[3/(x02 + y02)][y0/(x02 + y02)1/2] + (4/y02)}j
= Gm2{(2/x02) +[3x0/(x02 + y02)3/2]}i + Gm2{[3y0/(x02 + y02)3/2] + (4/y02)}j.
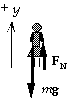
23. We take the positive direction upward. The spring scale reads the
normal force expressed as an effective mass:
FN/g.
We write Sum(F) = ma from the force diagram:
FN - mg = ma, or meffective = FN/g = m(1 + a/g).
(a) For a constant speed, there is no acceleration, so we have
meffective = m(1 + a/g) = m = 56 kg.
(b) For a constant speed, there is no acceleration, so we have
meffective = m(1 + a/g) = m = 56 kg.
(c) For the upward (positive) acceleration, we have
meffective = m(1 + a/g) = m(1 + 0.33g/g) = 1.33(56 kg) = 75 kg.
(d) For the downward (negative) acceleration, we have
meffective = m(1 + a/g) = m(1 - 0.33g/g) = 0.67(56 kg) = 38 kg.
(e) In free fall the acceleration is - g, so we have
meffective = m(1 + a/g) = m(1 - g/g) = 0.
33. From Kepler's third law,
T2 = 4p2r3/GmE,
we can relate the periods of the satellite and the Moon:
(T/TMoon)2 = (r/rMoon)3;
(T/27.4 d)2 = [(6.38x106 m)/(3.84x108 m)]3,
which gives:
T = 0.0587 days (1.41 h).
37. We use Kepler's third law, T2 = 4p2r3/GmE , for the motion of the Sun:
T2 = 4p2r3/Gmgalaxy;
= 4p2[(3x104 ly)(3x108 m/s)(3.16x107 s/yr)]3/(6.67x10-11 N · m2/kg2)(4x1041 kg),
which gives:
T = 6x1015 s = 2x108 yr.
57. (a) If we assume Eros is a cylinder, its mass is
meros = pr2h = (2.3x103 kg/m3)p(3x103 m)2(40x103 m) = 2.6x1015 kg.
We assume NEAR orbits around the narrow waist of Eros and use Kepler's third law:
T2 = 4p2r3/Gmeros
= 4p2[(15x103 m) + (3x103 m)]3/(6.67x10-11 N · m2/kg2)(2.6x1015 kg),
which gives
T = 3.6x104 s = 10 h.
(b) With the same mass and density, the sphere must have the same volume:
4/3pr03 = (40 km)p(3 km)2, which gives r0 = 6.5 km.
(c) The acceleration due to gravity on the surface of a spherical Eros is
g = Gmeros/r02
= (6.67x10-11 N · m2/kg2)(2.6x1015 kg)/(6.5x103 m)2 = 4.2x10-3 m/s2.

8. For the magnitude of each attractive
gravitational force, we have:
FV = GmEmV/rV2 = GfVmE2/rV2
= (6.67x10-11 N · m2/kg2)(0.815)(5.98x1024 kg)2/[(108 - 150)x109 m]2
= 1.10x1018 N;
FJ = GmEmJ/rJ2 = GfJmE2/rJ2
= (6.67x10-11 N · m2/kg2)(318)(5.98x1024 kg)2/[(778 - 150)x109 m]2
= 1.92x1018 N;
FSa = GmEmSa/rSa2 = GfSamE2/rSa2
= (6.67x10-11 N · m2/kg2)(95.1)(5.98x1024 kg)2/[(1430 - 150)x109 m]2
= 1.38x1017 N.
The force from Venus is toward the Sun;
the forces from Jupiter and Saturn are away from the Sun.
For the net force we have:
FNet = FJ + FSa - FV
= 1.92x1018 N + 1.38x1017 N - 1.10x1018 N
= 9.6x1017 N away from the Sun.
11. The weight of objects is determined by g, which depends on the mass and radius of the Earth:
g = GmE/rE2.
If the density remains constant, the mass will be proportional to the radius cubed:
mE'/mE = (rE'/rE)3.
If we form the ration of g's, we have
g'/g = (mE'/mE)/(rE'/rE)2 = (mE'/mE)/(mE'/mE)2/3 = (mE'/mE)1/3 = 21/3 = 1.26.
25. The acceleration due to gravity is
g = Fgrav/M = Gm/r2
= (6.67x10-11 N · m2/kg2)(7.4x1022 kg)/(4.1x106 m)2 = 0.29 m/s2.
We take the positive direction toward the Moon. The apparent weight
is measured by the normal force. We write Sum(F) = Ma from the force diagram:
- FN + Mg = Ma,
(a) For a constant velocity, there is no acceleration, so we have
- FN + Mg = 0, or
FN = Mg = (75 kg)(0.29 m/s2) = 22 N (toward the Moon).
(b) For an acceleration toward the Moon, we have
- FN + Mg = Ma, or
FN = M(g - a) = (75 kg)(0.29 m/s2 - 2.6 m/s2)
= - 1.7x102 N (away from the Moon).
45. (a) The gravitational field is
g = GmS/DSE2
= (6.67x10-11 N · m2/kg2)(2.0x1030 kg)/(1.50x1011 m)2
= 5.9x10-3 N/kg.
(b) Because the field due to the Sun is about 1000 times smaller
than the field from the Earth,
the effect is not significant.
60. We relate the speed to the period of revolution from
v = 2pr/T, where r is the distance to the center of the Milky Way.
The gravitational attraction provides the centripetal acceleration:
GmgalaxymS/r2 = mSv2/r = mS(2pr/T)2/r = mS4p2r/T2,
so we have:
mgalaxy = 4p2r3/GT2
= 4p2[(30,000 ly)(9.5x1015 m/ly)]3/
(6.67x10-11 N · m2/kg2)[(200x106 yr)(3.16x107 s/yr)]2
= 3.4x1041 kg.
The number of stars ("Suns") is
(3.4x1041 kg)/(2.0x1030 kg) = 1.7x1011.
62. The gravitational attraction from the core must provide the centripetal
acceleration for the orbiting stars:
Gmstarmcore/R2 = mstarv2/R,
so we have:
mcore = v2R/G
= (780x103 m/s)2(5.7x1017 m)/(6.67x10-11 N · m2/kg2)
= 5.2x1039 kg.
If we compare this to our Sun, we get
mcore/mSun = (5.2x1039 kg)/(2.0x1030 kg) = 2.6x109 X.
17. For a stationary object at the equator, we know that the effective weight is
w0 = mg - mvE2/rE ,
where vE = 2prE f is the speed of a point on the equator.
When the ship moves with respect to the surface at speed v,
the effective speed will be vE ± v, depending on the direction.
The positive sign is used for a ship traveling eastward; the negative sign for a ship traveling westward.
Thus the apparent weight is:
w = mg - m(vE ± v)2/rE = mg - (mvE2/rE)[1 ± (v/vE)]2 = mg - (mvE2/rE)[1 ± 2(v/vE) + (v/vE)2].
Because v << vE , we can drop the last term to get
w = mg - (mvE2/rE) - 2(mvEv/rE).
If we divide this by the effective weight for a stationary object, we have
w/w0 = [mg - (mvE2/rE) - 2(mvEv/rE)]/(mg - mvE2/rE) = 1 - 2(mvEv/rE)/(mg - mvE2/rE)
= 1 - 2(vEv/grE)/(1 - vE2/grE).
Because vE2/grE << 1, we get
w/w0 ~ 1 - 2(vEv/grE) ~ 1 ± 2(vEv/grE) = 1 ± 4pfv/g,
if we reverse the meaning of the sign for the direction of the ship:
positive sign is used for a ship traveling westward;
the negative sign for a ship traveling eastward.