Chapter 7 Solutions
13,21,23,34,52,55;15,24,51,53,56,67;38,74
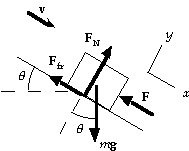
13. (a) From the force diagram, we write Sum(F) = ma:
y-component: FN - mg cosq = 0;
x-component: - F - mkFN + mg sinq = 0.
Thus we have
F = - mkFN + mg sinq = - mkmg cosq + mg sinq
= mg (sinq - mk cosq)
= (380 kg)(9.80 m/s2)(sin 27° - 0.40 cos 27°) = 3.6x102 N.
(b) Because the piano is sliding down the incline, we have
WF = F d cos 180° = (3.6x102 J)(3.5 m)(- 1) = - 1.3x103 J.
(c) For the friction force, we have
Wfr = mkmg cosq d cos 180°
= (0.40)(380 kg)(9.80 m/s2)(cos 27°)(3.5 m)(- 1) = - 4.6x103 J.
(d) For the force of gravity, we have
Wgrav = mg d cos 63°
= (380 kg)(9.80 m/s2)(3.5 m)(cos 63°) = 5.9x103 J.
(e) Because the normal force does no work, we have
Wnet = Wgrav + WF + Wfr + WN
= 5.9x103 J - 1.3 x103 J - 4.6x103 J + 0 = 0.
21. (a) A · (B + C) = (7.0 i - 8.5 j) · [(- 8.0 + 6.8) i + (8.1 - 7.2) j + 4.2 k]
= (7.0)(- 1.2) + (- 8.5)(0.9) = - 16.1.
(b) (A + C) · B = [(7.0 + 6.8) i + (- 8.5 - 7.2) j + 0 k] · (- 8.0 i + 8.1 j + 4.2 k)
= (13.8)(- 8.0) + (- 15.7)(8.1) + 0 = - 238.
(c) (B + A) · C = [(- 8.0 + 7.0) i + (8.1 - 8.5) j + (4.2 + 0) k] · (6.8 i - 7.2 j)
= (- 1.0)(6.8) + (- 0.4)(- 7.2) + (4.2)(0) = - 3.9.
23. Because C lies in the xy-plane and is perpendicular to B, we have
B · C = BxCx + ByCy = 9.6Cx + 6.7Cy = 0.
For the scalar product of A and C we have
A · C = AxCx + AyCy = - 4.8Cx + 7.8Cy = 20.0.
When we solve these two equations for the two unknowns, we get
Cx = -1.25, and Cy = 1.79.
Thus C = - 1.3i + 1.8j.
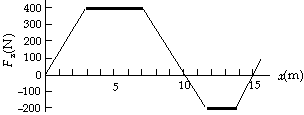
34. The work done in moving the object is the area
under the Fx vs. x graph.
(a) For the motion from 0.0 m to 10.0 m, we find
the area of two triangles and one rectangle:
W = 1/2(400 N)(3.0 m - 0.0 m)
+ (400 N)(7.0 m - 3.0 m) +
1/2(400 N)(10.0 m - 7.0 m)
= 2.8x103 J.
(b) For the motion from 0.0 m to 15.0 m, we add
the negative area of two triangles and one rectangle:
W = 2.8x103 J - 1/2(200 N)(11.7 m - 10.0 m) -
(200 N)(13.7 m - 11.7 m) - 1/2(200 N)(15.0 m - 13.7 m) = 2.1x103 J.
52. Because the force F holds the spring a distance x,
the spring constant is k = F/x. The work done by the
spring changes the kinetic energy of the mass:
Wspring = DK;
- (1/2kxf2 - 1/2kxi2) = 1/2mvf2 - 1/2mvi2.
(a) When the spring returns to xf = 0, we have
- (0 - 1/2kx2) = 1/2mvf2 - 0, or vf = (k/m)1/2x = (Fx/m)1/2.
(b) When the spring returns to xf = 1/2x, we have
- [1/2k(1/2x)2 - 1/2kx2] = 1/2mvf2 - 0, or vf = (3k/4m)1/2x = (3Fx/4m)1/2.
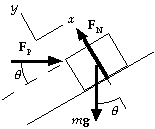
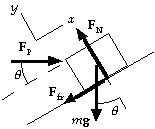
55. (a) For the work done by the applied force we have
WP = FP d cosq = (150 N) cos 30° (5.0 m) = 6.5x102 J.
(b) For the force of gravity, we have
Wgrav = (- mg sinq )d
= - (20 kg)(9.80 m/s2)(5.0 m) sin 30° = - 4.9x102 J.
(c) Because the normal force is perpendicular to the displacement,
it does no work: WN = 0.
(d) The net work done on the block increases its kinetic energy:
Wnet = WP + Wgrav + WN = 1/2mv2 - 1/2mv02 ;
6.5x102 J - 4.9x102 J + 0 = 1/2(20 kg)v2 - 0, which gives v = 4.0 m/s.
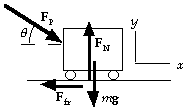
15. Because the motion is in the x-direction, we see that the
weight and normal forces do no work:
WFN = Wmg = 0.
From the force diagram, we write Sum(F) = ma:
x-component: FP cosq - Ffr = 0, or Ffr = FP cosq.
For the work by these two forces, we have
WFP = FP Dx cosq = (14 N)(15 m) cos 20° = 2.0x102 J.
Wfr = FP cosq Dx cos 180°= (14 N) cos 20° (15 m)(- 1) = - 2.0x102 J.
As expected, the total work is zero: WFP = - Wfr = 2.0x102 J.
24. For the sum and difference vectors, we have
Csum = A + B, Cdiff = A - B.
If we form the scalar product, we get
Csum · Cdiff = (A + B) · (A - B) = A · A + B · A - A · B - B · B = A2 - B2 = 0,
because A and B have the same magnitude.
Because the scalar product is zero, the sum and difference
vectors are perpendicular.
51. On the level the normal force is
FN = mg,
so the friction force is
Ffr = mkmg.
The normal force and the weight do no work.
The net work increases the kinetic energy of the mass:
Wnet = DK = 1/2mvf2 - 1/2mvi2;
F(L1 + L2) - mkmgL2 = 1/2mvf2 - 0;
(225 N)(11.0 m + 10.0 m) - (0.20)(66.0 kg)(9.80 m/s2)(10.0 m) = 1/2(66.0 kg)vf2,
which gives vf = 10.2 m/s.
53. There will be an additional (negative) work done by the friction force.
The net work increases the kinetic energy of the mass:
- (1/2kxf2 - 1/2kxi2) - mkmg Dx = 1/2mvf2 - 1/2mvi2;
- (0 - 1/2kx2) - mkmgx = 0 - 0,
which gives mk = kx/2mg = F/2mg.
56. (a) The work done by the applied force is the same:
WP = 6.5x102 J.
(b) The work done by gravity is the same: Wgrav = - 4.9x102 J.
(c) The work done by the normal force is the same: WN = 0.
(d) From the force diagram, we write Sum(F) = ma:
y-component: FN - mg cosq - FP sinq = 0, or
FN = mg cosq + FP sinq
= (20 kg)(9.80 m/s2) cos 30° + (150 N) sin 30° = 245 N.
The friction force is
Ffr = mkFN ,
so the work done by friction is
Wfr = - mkFNd
= - (0.10)(245 N)(5.0 m) = - 1.2x102 J.
The net work done on the block increases its kinetic energy:
Wnet = WP + Wgrav + WN + Wfr = 1/2mv2 - 1/2mv02 ;
6.5x102 J - 4.9x102 J + 0 - 1.2x102 J = 1/2(20 kg)v2 - 0, which gives v = 1.9 m/s.
67. The work done by the force is
W = F · d = Fx dx + Fy dy + Fz dz
= (10.0 kN)(5.0 m) + (9.0 kN)(4.0 m) + (12.0 kN)(0) = 86 kJ.
If we use the other expression for the scalar product, we have
W = F · d = Fd cosq;
86 kJ = [(10.0 kN)2 + (9.0 kN)2 + (12.0 kN)2]1/2[(5.0 m)2 + (4.0 m)2]1/2 cosq.
which gives
cosq = 0.746, q = 42°.
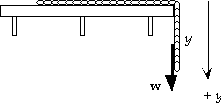
38. If we let y be the length of chain hanging over the edge and use
m for linear weight density, the weight hanging is w = my. As the
next differential length dy comes over the edge, the weight w
will fall a distance dy, during which the force of gravity will do
work dW = w dy. If L1 is the initial hanging length and L is the
total length of the chain, we integrate this from L1 to L:
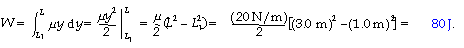
74. (a) The net work decreases the kinetic energy:
Wsnow + Wgrav = Wsnow + mgd = DK = 1/2mvf2 - 1/2mvi2;
Wsnow + (80 kg)(9.80 m/s2)(1.1 m) = 1/2(80 kg)[0 - (50 m/s)2] = - 1.0x105 J.
(b) We find the average force from
F = W/d = (- 1.0x105 J)/(1.1 m) = - 9.1x104 N.
(c) With air resistance during the fall we have
Wair + Wgrav = Wair + mgh = DK= (1/2mvf2 - 1/2mvi2)
Wair + (80 kg)(9.80 m/s2)(370 m) = 1/2(80 kg)[(50 m/s)2 - 0], which gives Wair =
- 1.9x105 J.





