Chapter 8 Solutions
15,27,32,43,49,79; 20,29,42,73,87,97; 53

15.(a) For the motion from the bridge to the lowest point, we use
energy conservation:
Ki + Ugrav i + Ucord i = Kf + Ugrav f + Ucord f ;
0 + 0 + 0 = 0 + mg(- h) + 1/2k(h - L0)2 ;
0 = - (60 kg)(9.80 m/s2)(31 m) + 1/2k(31 m - 12 m)2,
which gives k = 1.0x102 N/m.
(b)The maximum acceleration will occur at the lowest point,
where the upward restoring force in the
cord is maximum:
kxmax - mg = mamax ;
(1.0x102 N/m)(31 m - 12 m) - (60 kg)(9.80 m/s2) = (60 kg)amax ,
which gives amax = 22 m/s2.
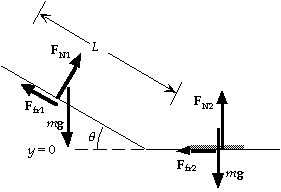
27.(a)We find the normal force from the force diagram for the ski:
y-component: FN1 = mg cos q;
which gives the friction force: Ffr1 = mkmg cos q.
For the work-energy principle, we have
WNC = DK + DU = (1/2mvf2 - 1/2mvi2) + mg(hf - hi);
- mkmg cos q L = (1/2mvf2 - 0) + mg(0 - L sin q);
- (0.090)(9.80 m/s2) cos 20o (100 m) =
1/2vf2 - (9.80 m/s2)(100 m) sin 20D,
which gives vf = 22 m/s.
(b) On the level the normal force is FN2 = mg, so the
friction force is Ffr2 = mkmg.
For the work-energy principle, we have
WNC = DK + DU = (1/2mvf2 - 1/2mvi2) + mg(hf - hi);
- mkmg D = (0 - 1/2mvi2) + mg(0 - 0);
- (0.090)(9.80 m/s2)D = - 1/2(22.5 m/s)2 ,
which gives D = 2.9x102 m.
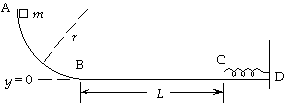
32.(a)For the motion from A to B, there is no
friction and the normal force does no work.
For the work-energy principle, we have
WNC = (1/2mvB2 - 1/2mvA2) + mg(hB - hA);
0 = 1/2mvB2 - 0 + 0 - mgr;
0 = 1/2vB2 - (9.80 m/s2)(2.0 m),
which gives vB = 6.3 m/s.
(b)On the level the normal force is FN = mg,
so the friction force is Ffr = mkmg.
The work done by this force from B to C is
WNC = - mkmgL
= - (0.25)(1.0 kg)(9.80 m/s2)(3.0 m) = - 7.4 J.
(c)For the motion from B to C, the normal force does no work. For the work-energy principle, we have
WNC = (1/2mvC2 - 1/2mvB2) + mg(hC - hB);
- 7.4 J = 1/2(1.0 kg)vC2 - 1/2(1.0 kg)(6.3 m/s)2 + 0 - 0,
which gives vC = 4.9 m/s.
(d)For the motion from C to the point where the block momentarily comes to rest, there is no friction.
For the work-energy principle, we have
WNC = (1/2mv2 - 1/2mvC2) + mg(h - hC) + (1/2kx2 - 1/2kxC2);
0 = 0 - 1/2(1.0 kg)(4.9 m/s)2 + 0 - 0 + 1/2k(0.20 m)2 - 0,
which gives k = 6.1x102 N/m.
43. The escape velocity for a mass m is the speed required so the mass can get infinitely far away with essentially zero velocity. From energy conservation we have
K1 + U1 = K2 + U2 ;
1/2mvesc2 - GMEm/r = 0 - GMEm/D, or vesc2 = 2GME/r.
Because the gravitational attraction provides the radial acceleration of the satellite, we have
GmME/r2 = mvorbit2/r, or vorbit2 = GME/r.
For the ratio we get
vesc2/vorbit2 = (2GME/r )/(GME/r), or vesc/vorbit = (2)1/2.
49. The total energy of the satellite in an orbit of radius r is
E = K + U = 1/2mv2 - GMEm/r = 1/2mGME/r - GMEm/r = - 1/2mGME/r.
Thus the work required is
W = DE = - 1/2mGME[(1/r2) - (1/r1)]
= - 1/2mGME[(1/3rE) - (1/2rE)] = GmME/12rE.
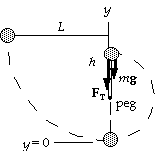
79. We choose the reference level for the gravitational potential
energy at the lowest point. The tension in the cord is always
perpendicular to the displacement and thus does no work.
(a)With no air resistance during the fall, we have
0 = DK + DU = (1/2mv12 - 1/2mv02) + mg(h1 - h0), or
1/2(v12 - 0) = - g(0 - L), which gives v1 = (2gL)1/2.
(b)For the motion from release to the rise around the peg, we have
0 = DK + DU = (1/2mv22 - 1/2mv02) + mg(h2 - h0), or
1/2(v22 - 0) = - g[2(L - h) - L] = g(2h - L) = 0.60gL,
which gives v2 = (1.2gL)1/2.
20.(a)The work done against gravity is the increase in the potential energy:
W = mgh = (75.0 kg)(9.80 m/s2)(92.0 m) = 6.76x104 J.
(b)If this work is done by the force on the pedals, we need to find the distance that the force acts
over one revolution of the pedals and the number of revolutions to climb the hill. We find the
number of revolutions from the distance along the incline:
N = (h/ sin q)/(5.10 m/revolution)
= [(92.0 m)/ sin 9.50o]/(5.10 m/revolution) = 109 revolutions.
Because the force is always tangent to the circular path, in each revolution the force acts over a
distance equal to the circumference of the path: pD. Thus we have
W = NFpD;
6.76x104 J = (109 revolutions)Fp(0.360 m), which gives F = 547 N.
29. On the level the normal force is FN = mg, so the friction force is Ffr = mkmg.
For the work-energy principle, we have
WNC = DK + DU = (1/2mvf2 - 1/2mvi2) + mg(hf - hi);
F(L1 + L2) - mkmg L2 = (1/2mvf2 - 0) + mg(0 - 0);
(350 N)(15 m + 15 m) - (0.25)(90 kg)(9.80 m/s2)(15 m) = 1/2(90 kg)vf2,
which gives vf = 13 m/s.
42.(a)Because the gravitational attraction provides the radial acceleration of the satellite, we have
GmME/r2 = mv2/r, or v2 = GME/r.
The total energy of the satellite is
E = K + U = 1/2mv2 - GMEm/r = 1/2mGME/r - GMEm/r = - 1/2GmME/r.
(b)From the expression for the total energy, we see that a decrease in E (E becomes more negative)
means a decrease in r. Because the kinetic energy is positive, a decrease in r means an increase in
kinetic energy.
73. We choose the potential energy to be zero at the initial level of the center of mass (y = 0).
We find the minimum speed by ignoring any frictional forces. Energy is conserved, so we have
E = Ki + Ui = Kf + Uf ;
1/2mvi2 + mgyi = 1/2mvf2 + mgyf ;
1/2mvi2 + m(9.80 m/s2)(0) = 1/2m(6.5 m/s)2 + m(9.80 m/s2)(1.1 m), which gives vi = 8.0 m/s.
Note that the initial velocity will not be horizontal, but will have a horizontal component of 6.5 m/s.
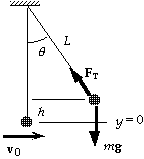
87. We choose the potential energy to be zero at the lowest point (y = 0).
(a)Because the tension in the rope does no work, energy is conserved,
so we have
Ki + Ui = Kf + Uf;
1/2mv02 + 0 = 0 + mgh = mg(L - L cos q) = mgL(1 - cos q);
1/2m(5.0 m/s)2 = m(9.80 m/s2)(10.0 m)(1 - cos q)
which gives cos q = 0.872, or q = 29o.
(b)The velocity is zero just before he releases, so there is no centripetal
acceleration. There is a tangential acceleration which has been
decreasing his tangential velocity. For the radial direction we have
FT - mg cos q = 0; or
FT = mg cos q = (75 kg)(9.80 m/s2)(0.872) = 6.4x102 N.
(c)The velocity and thus the centripetal acceleration is maximum at the bottom, so the tension will be
maximum there. For the radial direction we have
FT - mg = mv02/L, or
FT = mg + mv02/L = (75 kg)[(9.80 m/s2) + (5.0 m/s)2/(10.0 m)] = 9.2x102 N.
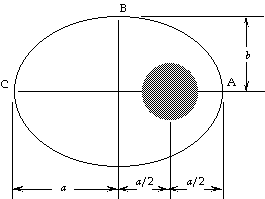
97.(a)At point B the distance of the satellite from
the center of the Earth is
rB = [(1/2a)2 + b2]1/2
= [(8,000 km)2 + (13,900 km)2]1/2
= 16,000 km.
For energy conservation for the motion from A to B,
we have
KA + UA = KB + UB ;
1/2mvA2 - GMEm/rA = 1/2mvB2 - GMEm/rB , or
vB2 = vA2 + 2GME(1/rB - 1/rA);
vB2 = (8650 m/s)2 + 2(6.67x10-11 N * m2/kg2) x
(5.98x1024 kg)[(1/16.0x106 m) - (1/8.0x106 m)]
which gives vB = 5.00x103 m/s.
(b)For energy conservation for the motion from A to C, we have
KA + UA = KC + UC ;
1/2mvA2 - GMEm/rA = 1/2mvC2 - GMEm/rC , or
vC2 = vA2 + 2GME[1/(*a) - 1/(1/2a)];
vC2 = (8650 m/s)2 + 2(6.67x10-11 N * m2/kg2)(5.98x1024 kg)[(1/24.0x106 m) - (1/8.0x106 m)]
which gives vC = 2.89x103 m/s.
53. The escape speed from the surface of the Earth, ignoring the Sun, is found from
vE2 = 2GME/rE = 2(6.67x10-11 N * m2/kg2)(5.98x1024 kg)/(6.38x106 m),
which gives vE = 1.12x104 m/s = 11.2 km/s.
The escape speed from the Sun when at the Earth's orbit, ignoring the Earth, is found from
vS2 = 2GMS/rSE
= 2(6.67x10-11 N * m2/kg2)(2.0x1030 kg)/(1.50x1011 m),
which gives vS = 4.22x104 m/s = 42.2 km/s.
The orbital speed of the Earth is
vO = rSEw = (1.50x1011 m)(2p rad/yr)/(3.17x107 s/yr) = 2.98x104 m/s = 29.8 km/s.
(a)In the reference frame of the Earth, if the spacecraft leaves the surface of the Earth with speed v,
we find the speed v' at a distance where the gravitational attraction is negligible from energy
conservation:
K1 + U1 = K2 + U2 ;
1/2mv2 - GMEm/rE = 1/2mv'2 - 0, or
v2 = v'2 + 2GME/rE = v'2 + vE2.
The reference frame of the Earth is orbiting the Sun with speed vO . In the reference frame of the Sun,
the speed far from the Earth is
vS = v' + vO .
When we use this in the previous result, we get
v2 = (vS - vO)2 + vE2, or
v = [vE2 + (vS - vO)2]1/2 = [(11.2 km/s)2 + (42.2 km/s - 29.8 km/s)2]1/2 = 16.7 km/s.
(b)The required kinetic energy is
K = 1/2mv2, so we have
K/m = 1/2v2 = 1/2(1.67x104 m/s)2 = 1.40x108 J/kg.





