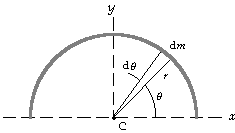Chapter 9 Solutions
13,26,35,49,61,75; 14,30,41,42,69,74; 65
13. During the throwing we use momentum conservation for the one-dimensional motion:
0 = (mboat + mchild)vboat + mpackagevpackage ;
0 = (55.0 kg + 26.0 kg)vboat + (5.40 kg)(10.0 m/s), which gives
vboat = - 0.667 m/s (opposite to the direction of the package).
26. In the reference frame of the capsule before the push, we take the positive direction in the direction the capsule will move.
(a) Momentum conservation gives us
mvastronaut + Mvsatellite = mv'astronaut + Mv'satellite,
0 + 0 = (140 kg)(- 2.50 m/s) + (1800 kg) v'satellite, which gives v'satellite= 0.194 m/s.
(b) We find the force on the satellite from
Fsatellite = Dpsatellite/Dt = msatellite Dvsatellite/Dt
= (1800 kg)(0.194 m/s - 0)/(0.500 s) = 700 N.
There will be an equal but opposite force on the astronaut.
(c) The kinetic energies are
Kastronaut = 1/2m v'astronaut2 = 1/2(140 kg)(2.50 m/s)2 = 438 J.
Ksatellite = 1/2M v'satellite2 = 1/2(1800 kg)(0.194 m/s)2 = 33.9 J.
35. (a) For the elastic collision of the two balls, we use momentum conservation for this
one-dimensional motion:
m1v1 + m2v2 = m1v1' + m2v2';
(0.220 kg)(6.5 m/s) + m2(0) = (0.220 kg)(- 3.8 m/s) + m2v2'.
Because the collision is elastic, the relative speed does not change:
v1 - v2 = - (v1' - v2'), or 6.5 m/s - 0 = v2' - (- 3.8 m/s),
which gives v2' = 2.7 m/s.
(b) Using the result for v2' in the momentum equation, we get m2 = 0.84 kg.
49. For the momentum conservation of this one-dimensional collision, we have
m1v1 + m2v2 = m1v1' + m2v2'.
(a) If the bodies stick together, v1' = v2' = V:
(5.0 kg)(5.5 m/s) + (3.0 kg)(- 4.0 m/s) = (5.0 kg + 3.0 kg)V, which gives V = v1' = v2' = 1.9 m/s.
(b) If the collision is elastic, the relative speed does not change:
v1 - v2 = - (v1' - v2'), or 5.5 m/s - (- 4.0 m/s) = 9.5 m/s = v2' - v1'.
The momentum equation is
(5.0 kg)(5.5 m/s) + (3.0 kg)(- 4.0 m/s) = (5.0 kg)v1' + (3.0 kg)v2', or
(5.0 kg)v1' + (3.0 kg)v2' = 15.5 kg * m/s.
When we combine these two equations, we get v1' = - 1.6 m/s, v2' = 7.9 m/s.
(c) If m1 comes to rest, v1' = 0.
(5.0 kg)(5.5 m/s) + (3.0 kg)(- 4.0 m/s) = 0 + (3.0 kg)v2', which gives v1' = 0, v2' = 5.2 m/s.
(d) If m2 comes to rest, v2' = 0.
(5.0 kg)(5.5 m/s) + (3.0 kg)(- 4.0 m/s) = (5.0 kg)v1' + 0, which gives v1' = 3.1 m/s, v2' = 0.
(e) The momentum equation is
(5.0 kg)(5.5 m/s) + (3.0 kg)(- 4.0 m/s) = (5.0 kg)(- 4.0 m/s) + (3.0 kg)v2',
which gives v1' = - 4.0 m/s, v2' = 12 m/s.
The result for (c) is reasonable. The 3.0-kg body rebounds.
The result for (d) is not reasonable. The 5.0-kg body would have to pass through the 3.0-kg body.
To check the result for (e) we find the change in kinetic energy:
DK = (1/2m1v1'2 + 1/2m2v2'2) - (1/2m1v12 + 1/2m2v22)
= 1/2[(5.0 kg)(- 4.0 m/s)2 + (3.0 kg)(12 m/s)2] - 1/2[(5.0 kg)(5.5 m/s)2 + (3.0 kg)(- 4.0 m/s)2]
= + 156 J.
Because the kinetic energy cannot increase in a simple collision, the result for (e) is not reasonable.
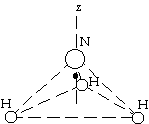
61. From the symmetry of the hydrogen triangle, we know that the center
of mass will be perpendicular to the plane of the hydrogen atoms along
a line from the center of the triangle. We find the height above the
triangle from
zCM = [3mH(0) + mNzN]/(3mH + mN)
= [0+ (14 u)(0.037 nm)]/[(3(1 u) + 14 u]
= 0.030 nm above center of H triangle.
75. We find the time for the man to reach the other end from
t = L/vrel = (25 m)/(2.0 m/s) = 12.5 s.
If we let v2 be the speed of the flatcar while the man is walking, the speed of the man is v1 = v2 + vrel.
Because the velocity of the center of mass of the system of flatcar and man does not change, we have
vCM = (m1v1 + m2v2)/(m1 + m2)
5.0 m/s = [(90 kg)(v2 + 2.0 m/s) + (200 kg)v2]/(90 kg + 200 kg), which gives v2 = 4.38 m/s.
The flatcar will have moved
x = v2t = (4.38 m/s)(12.5 s) = 55 m.
14. Momentum conservation gives us
mv1 + Mv2 = mv1' + Mv2',
(0.012 kg)(190 m/s) + 0 = (0.012 kg)(150 m/s) + (2.0 kg)v2',
which gives v2' = 0.24 m/s.
30. The maximum force that each leg can exert without breaking is
(170x106 N/m2)(2.5x10-4 m2) = 4.25x104 N,
so, if there is an even landing with both feet, the maximum force allowed on the body is 8.50x104 N.
We use the work-energy principle for the fall to find the landing speed:
0 = DK + DU;
0 = 1/2mvland2 - 0 + (0 - mghmax), or vland2 = 2ghmax .
The impulse from the maximum force changes the momentum on landing.
If we take down as the positive direction and assume the landing lasts for a time t, we have
- Fmaxt = m Dv = m(0 - vland), or t = mvland/Fmax .
We have assumed a constant force, so the acceleration will be constant. For the landing we have
y = vlandt + 1/2at2 = vland(mvland/Fmax) + 1/2(- Fmax/m)(mvland/Fmax)2 = 1/2mvland2/Fmax = mghmax/Fmax ;
0.60 m = (75 kg)(9.80 m/s2)hmax/(8.50x104 N), which gives hmax = 69 m.
41. (a) At the maximum compression of the spring, there will be no relative motion of the two blocks.
Because there is no friction, we can use momentum conservation:
m1v1 + m2v2 = m1v1' + m2v2';
m1v1 + 0 = (m1 + m2)V, or V = m1v1/(m1 + m2).
Energy is also conserved, so we have
1/2m1v12 + 0 = 1/2(m1 + m2)V2 + 1/2kx2;
1/2m1v12 = 1/2(m1 + m2)[m1v1/(m1 + m2)]2 + 1/2kx2, or
x2 = m1m2v12/k(m1 + m2) = (2.0 kg)(4.5 kg)(8.0 m/s)2/(850 N/m)(2.0 kg + 4.5 kg),
which gives x = 0.32 m.
(b) From the initial motion of the first block to the final separation, all horizontal forces are internal
to the system of the two blocks and are conservative. For momentum conservation we have
m1v1 + m2v2 = m1v1' + m2v2';
m1v1 + 0 = m1v1' + m2v2'.
Because the collision is elastic, the relative speed does not change:
v1 - v2 = - (v1' - v2'), or v2' = v1 - 0 + v1'.
When we combine the equations, we get
v1' = (m1 - m2)v1/(m1 + m1) = (2.0 kg - 4.5 kg)(8.0 m/s)/(2.0 kg + 4.5 kg) = - 3.1 m/s (rebound).
For v2' we get
v2' = v1 + v1' = 8.0 m/s + (- 3.1 m/s) = 4.9 m/s.
(c) Yes, because the force by the spring is conservative, the collision is elastic.
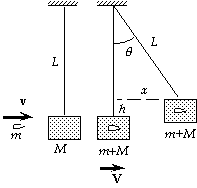
42. We let V be the speed of the block and bullet immediately
after the collision and before the pendulum swings. For this
perfectly inelastic collision, we use momentum conservation:
mv + 0 = (M + m)V;
(0.018 kg)(180 m/s) = (0.018 kg + 3.6 kg)V,
which gives V = 0.896 m/s.
Because the tension does no work, we can use energy conservation
for the swing:
1/2(M + m)V2 = (M + m)gh, or V2 = 2gh;
(0.896 m/s)2 = 2(9.80 m/s2)h, which gives h = 0.0409 m.
We find the horizontal displacement from the triangle:
L2 = (L - h)2 + x2;
(2.8 m)2 = (2.8 m - 0.0409 m)2 + x2, which gives x = 0.48 m.
69. (a) If we choose the origin at the center of the Earth, we have
xCM = (mEarthxEarth + mMoonxMoon)/(mEarth + mMoon)
= [0 + (7.35x1022 kg)(3.84x108 m)]/(5.98x1024 kg + 7.35x1022 kg)
= 4.66x106 m.
Note that this is less than the radius of the Earth and thus is inside the Earth.
(b) The CM found in part (a) will move around the Sun on an elliptical path. The Earth and Moon will
revolve about the CM. Because this is near the center of the Earth, the Earth will essentially be on
the elliptical path around the Sun. The motion of the Moon about the Sun is more complicated.
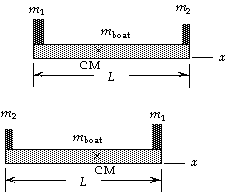
74. We choose the origin of our coordinate system at the
initial position of the 75-kg person. For the location of
the center of mass of the system we have
xCM = (m1x1 + m2x2 + mboatxboat)/(m1 + m2 + mboat)
= [(75 kg)(0) + (55 kg)(3.0 m) + (80 kg)(1.5 m)]/
(75 kg + 55 kg + 80 kg) = 1.36 m.
Thus the center of mass will be 3.0 m - 1.36 m = 1.64 m from
the 55-kg person. When the two people exchange seats,
the center of mass will not move. The end where the 75-kg
person started, which was 1.36 m from the center of mass,
is now 1.64 m from the center of mass, that is, the boat
must have moved 1.64 m - 1.36 m =
0.28 m toward the initial position of the 75-kg person.
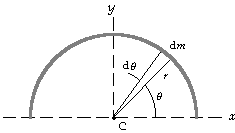
65. We know from the symmetry that the center of mass
lies on the y-axis: xCM = 0.
We choose a differential length of the wire r dq,
shown in the diagram, which has a mass dm = (m/pr)r dq.
We integrate over the wire to find yCM:
Thus the center of mass is at xCM = 0, yCM = 2r/p.