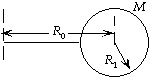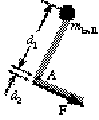Chapter 10 Solutions
13,23,30,45,65,75; 18,24,31,46,92,105; 79

13. The final angular speed is
w = (1 rpm)(2p rad/rev)/(60 s/min) = 0.105 rad/s.
(a) We find the angular acceleration from
a = Dw/Dt
= (0.105 rad/s - 0)/(10.0 min)(60 s/min) = 1.75 x10-4rad/s2.
(b) We find the angular speed after 5.0 min:
w = w0 + at = 0 + (1.75 x10-4rad/s2)(5.0 min)(60 s/min) = 5.25 x10-2rad/s.
At this time the radial acceleration of a point on the skin is
aR = w2r = (5.25 x10-2rad/s)2(4.25 m) = 1.17 x10-2m/s2.
The tangential acceleration is
atan = ar = (1.75 x10-4rad/s2)(4.25 m) = 7.44 x10-4m/s2.
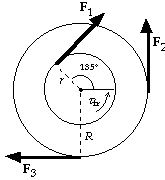
23. We assume clockwise motion, so the frictional torque is counterclockwise.
If we take the clockwise direction as positive, we have
tnet = rF1 - RF2 + RF3 - tfr
= (0.10 m)(35 N) - (0.20 m)(30 N) + (0.20 m)(20 N) - 0.30 m · N
= 1.2 m · N (clockwise).
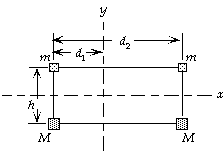
30. (a) For the moment of inertia about the y-axis, we have
Ia = SmiRi2 = md12 + Md12 + m(d2 - d1)2 + M(d2 - d1)2
= (1.8 kg)(0.50 m)2 + (3.1 kg)(0.50 m)2 +
(1.8 kg)(1.00 m)2 + (3.1 kg)(1.00 m)2 = 6.1 kg · m2.
(b) For the moment of inertia about the x-axis, all the masses
are the same distance from the axis, so we have
Ib = SmiRi2 = (2m + 2M)(1/2h)2
= [2(1.8 kg) + 2(3.1 kg)](0.25 m)2 = 0.61 kg · m2.
It will be harder to accelerate the array around the y-axis, because the moment of inertia is greater.
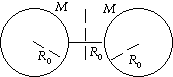
45. (a) We use the parallel-axis theorem:
I = 2(ICM + Mh2) = 2[(2MR02/5) + M(3R0/2)2] = 5.30MR02.
(b) If we treat the spheres as point masses, we get
I' = 2[M(3R0/2)2] = 4.50MR02.
The error is
error = (I' - I)/I = (4.50 - 5.30)/(5.30) = - 0.15 = - 15%.
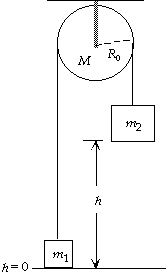
65. For the system of the two blocks and pulley, no work will be
done by nonconservative forces. The rope ensures that each
block has the same speed v and the angular speed of the
pulley is w = v/R0. We choose the reference level for
gravitational potential energy at the floor.
The rotational inertia of the pulley is I = 1/2MR02.
For the work-energy principle we have
Wnet = DK + DU;
0 = [(1/2m1v2 + 1/2m2v2 + 1/2Iw2) - 0] + m1g(h - 0) + m2g(0 - h);
1/2m1v2 + 1/2m2v2 + 1/2(1/2MR02)(v/R0)2 = (m2 - m1)gh;
1/2[m1 + m2 + 1/2M]v2 = (m2 - m1)gh;
1/2[35.0 kg + 38.0 kg + 1/2(4.8 kg)]v2 =
(38.0 kg - 35.0 kg)(9.80 m/s2)(2.5 m), which gives
v = 1.4 m/s.
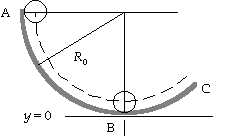
75. If the ball rolls without slipping, the speed of the center of
mass is v = r0w. Because energy is conserved, for the motion
from A to B we have
0 = DK + DU;
0 = [(1/2mv2 + 1/2Iw2) - 0] + (mgr0 - mgR0), or
1/2mv2 + 1/2(2/5 mr02)(v/r0)2 = mg(R0 - r0), which gives
v = [10g(R0 - r0)/7]1/2.
18. We find the initial and final angular velocities of the wheel from the rolling condition:
w0 = v0/r = [(90.0 km/h)/(3.6 ks/h)]/(0.45 m) = 55.6 rad/s;
w = v/r = [(60.0 km/h)/(3.6 ks/h)]/(0.45 m) = 37.0 rad/s.
(a) We find the angular acceleration from
w2 = w02 + 2aq;
(37.0 rad/s)2 = (55.6 rad/s)2 + 2a (85 rev)(2p rad/rev), which gives a= - 1.6 rad/s2.
(b) We find the additional time from
wfinal = w + at;
0 = 37.0 rad/s + (- 1.6 rad/s2)t, which gives t = 23 s.
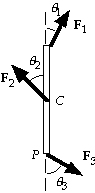
24. (a) We let L be the length of the beam and take clockwise as the
positive direction. For the net torque about point C, we have
tC = 1/2L(F1 sin q1) - 1/2L(F3 sin q3)
= 1/2(2.0 m)(50 N) sin 30° - 1/2(2.0 m)(50 N) sin 60°
= - 18 m · N (CCW=counter-clock-wise).
(b) For the net torque about point P, we have
tP = L(F1 sin q1) - 1/2L(F2 sin q2)
= (2.0 m)(50 N) sin 30° - 1/2(2.0 m)(60 N) sin 45°
= 7.6 m · N (CW=clockwise).
(See FIGURE 10-56)
31. For the moment of inertia of the rotor blades we have
I = 3(1/3mbladeL2) = mbladeL2 = (160 kg)(3.75 m)2 = 2.25 x103kg · m2.
We find the required torque from
t = Ia = I(w - w0)/t
= (2.25 x10-3kg · m2)[(5.0 rev/s)(2p rad/rev) - 0]/(8.0 s) = 8.8 x103m · N.
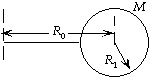
46. (a) If we treat the sphere as a point mass, we get
Ia = MR02.
(b) We use the parallel-axis theorem:
Ib = ICM + Mh2 = (2MR12/5) + MR02.
(c) The error is
error = (Ia - Ib)/Ib
= [MR02 - (2MR12/5) - MR02]/[(2MR12/5) + MR02]
= [- (2R12/5)]/[(2R12/5) + R02]
= - (0.40)(0.10 m)2/[(0.40)(0.10 m)2 + (1.0 m)2] = - 0.0040 = - 0.40%.
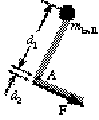
92. (a) The angular acceleration of the ball-arm system is
a = atan/d1 = (7.0 m/s2)/(0.30 m) = 23.3 rad/s2.
Because we ignore the mass of the arm, for the moment of
inertia we have
I = mballd12 = (1.00 kg)(0.30 m)2 = 0.090 kg · m2.
Thus we find the required torque from
t = Ia
= (0.090 kg · m2)(23.3 rad/s2) = 2.1 m · N.
(b) Because the force from the triceps muscle is perpendicular
to the line from the axis, we find the force from
F = t/d2 = (2.1 m · N)/(0.025 m) = 84 N.
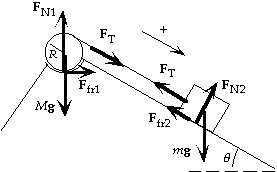
105. (a) The speed of the block is the tangential speed
of the cylinder, so v = Rw. For the system of
block and cylinder, if there is no friction, energy
is conserved. After the block has moved a
distance D, we have
0 = DK + DU;
0 = [(1/2mv2 + 1/2I1w2) - 0] + (0 - mgD sin q);
1/2mv2 + 1/2(1/2MR2)(v/R)2 = mgD sin q;
1/2mv2 + 1/4Mv2 = mgD sin q;
[1/2(3.0 kg) + 1/4(30 kg)]v2 =
(3.0 kg)(9.80 m/s2)(1.80 m) sin 30°,
which gives
v = 1.7 m/s.
(b) From the force diagram for the block we see that
Ffr2 = mFN2 = mmg cos q.
For the cylinder, we assume a single vertical normal force. Because there is no linear acceleration
of the center of mass, we have
FN1 = Mg + FT sin q.
Because the block accelerates down the plane, FT < mg sin D, and m = 0.1M. Thus we ignore the
contribution of FT sin q (and we are justified in ignoring the horizontal component of FN1) to get
FN1 ~ Mg, and Ffr1 = mFN1 = mMg.
When the block moves a distance D, the surface of the rotating cylinder will move a distance D
through the depression. For the work-energy theorem we have
Wfr = DK + DU;
- Ffr1D - Ffr2D = [(1/2mv2 + 1/2I1w2) - 0] + (0 - mgD sin q);
- m(M + m cos q)gD = 1/2mv2 + 1/4Mv2 - mgD sin q;
- (0.035)[30 kg + (3.0 kg) cos 30°](9.80 m/s2)(1.80 m) =
[1/2(3.0 kg) + 1/4(30 kg)]v2 - (3.0 kg)(9.80 m/s2)(1.80 m) sin 30°,
which gives
v = 0.84 m/s.
(See FIGURE 10-44)
79. (a) From Example 10-24, we see that while the ball is slipping, the acceleration of the center of mass
is - mkg and is constant. The ball slips for a time T = 2v0/7mkg, so we find the distance from
xslip = v0t + 1/2at2
= v0(2v0/7mkg) + 1/2(- mkg)(2v0/7mkg)2 = 12v02/49mkg.
(b) Once the ball starts rolling at time T, the linear speed is constant
v = v0 + at = v0 + (- mkg)(2v0/7mkg) = 5v0/7.
We can find the angular speed from
w = w0 + at, or from
w = v/R = (5v0/7)/R = 5v0/7R