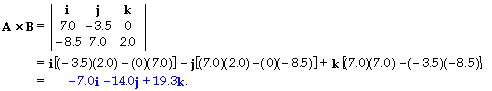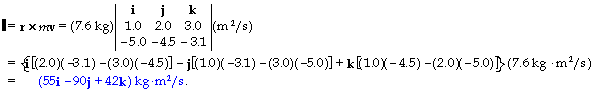Chapter 11 Solutions
Problems: 7,18,25,35,57,59; 10,19,26,36,60,63; 39
7. (a) For the vectors A = 7.0i - 3.5j and B = - 8.5i + 7.0j + 2.0k, we have
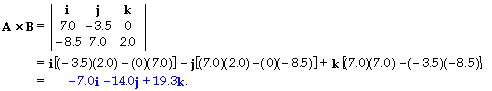
(b) The magnitudes of the vectors are
A = [(7.0)2 + (- 3.5)2]1/2 = 7.83;
B = [(- 8.5)2 + (7.0)2 + (2.0)2]1/2 = 11.2;
|A x B| = [(- 7.0)2 + (- 14.0)2 + (19.3)2]1/2 = 24.8.
We find the angle between A and B from
|A x B| = |A| |B| sinq ;
24.8 = (7.83)(11.2) sinq , which gives sinq = 0.283,
which gives q = 16o, 164o. From the diagram, we see that q = 164o.
18. For the angular momentum we have
L= r x mv = m(r x v)
= (0.060 kg)[(7.0 m)i + (- 6.0 m)j] ? [(2.0 m/s)i - (8.0 m/s) k]
= (0.060 kg){[(- 6.0 m)(- 8.0 m/s) - 0]i + [0 - (7.0 m)(- 8.0 m/s)]j + [0 - (- 6.0 m)(2.0 m/s)]k}
= (2.9i + 3.4j + 0.72k) kg * m2/s.
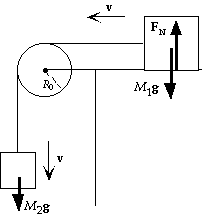
25. (a) With the positive direction CCW, for the angular
momentum about the axis of the pulley we have
L = R0M1v + R0M2v + Iw
= R0M1v + R0M2v + I(v/R0) = [R0M1 + R0M2 + (I/R0)]v.
(b) Because M1g is balanced by the normal force on the horizontal
surface, the net torque is from M2g only:
t = dL/dt;
M2gR0 = [R0M1 + R0M2 + (I/R0)] dv/dt, which gives
a = M2g/[M1 + M2 + (I/R02)].
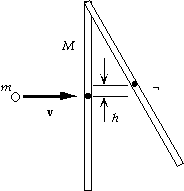
35. In the collision, during which we ignore any motion of the rod,
angular momentum about the pivot point will be conserved:
Li = Lf ;
mv(r/2) + 0 = Itotalw = [1/3Mr2 + m(1/2r)2]w, which gives
w = 6mv/(4M + 3m)r.
For the rotation about the pivot after the collision, energy will be
conserved. If the center of the rod reaches a height h, the bottom
of the rod will swing to a height H = 2h, so we have
Ki + Ui = Kf + Uf ;
1/2Itotalw2 + 0 = 0 + (m + M)gh;
1/2[1/3Mr2 + m(1/2r)2][6mv/(4M + 3m)r]2 = (m + M)gH/2,
which gives H = 3m2v2/g(3m + 4M)(m + M).
57. (a) The angular momentum delivered to the waterwheel in a time Dt is that lost by the water:
DL/Dt = Dm R(vi - vf)/Dt = (Dm/Dt)R(vi - vf)
= (150 kg/s)(3.0 m)(7.0 m/s - 3.0 m/s) = 1.8 x 103 kg * m2/s2.
(b) The torque applied to the waterwheel increases the angular momentum:
t = DL/Dt = 1.8 x 103 m * N.
(c) The power delivered is
P = tw = (1.8 x 103 m * N)(2p/5.5 s) = 2.1 x 103 W.
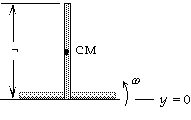
59. Because there is no friction, the center of mass must fall straight down.
The vertical velocity of the right end of the stick must always be zero.
If w is the angular velocity of the stick just before it hits the table, the
velocity of the right end with respect to the center of mass will be
w(r/2) up. Thus we have
w(r/2) - vCM = 0, or w = 2vCM/r.
The kinetic energy will be the translational energy of the center of mass
and the rotational energy about the center of mass. With the reference
level for potential energy at the ground, we use energy conservation to
find the speed of the center of mass just before the stick hits the ground:
Ki + Ui = Kf + Uf;
0 + Mg1/2r = 1/2MvCM2 + 1/2(Mr2/12)w2 + 0;
Mg1/2r = 1/2MvCM2 + 1/2(Mr2/12)(2vCM/r)2 = 1/2(4MvCM2/3), which gives vCM = (3gr/4)1/2 .
10. For the torque we have
t = r x F = [(4.0i + 8.0j + 6.0k) m] x [(16.0j - 4.0k) N]
= {[(8.0)(- 4.0) - (6.0)(16.0)]i + [0 - (4.0)(- 4.0)]j + [(4.0)(16.0) - 0]k} m * N
= (- 128i + 16j + 64k) m * N.
19. For the angular momentum we have
L=
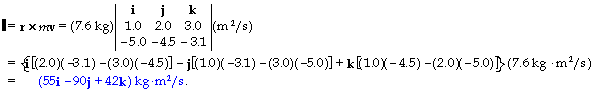
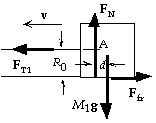
26. (a) With the positive direction CCW, we have the same
formula for the angular momentum:
L = [R0M1 + R0M2 + (I/R0)]v.
(b) Because M1g is balanced by the normal force on the horizontal
surface, the friction force is Ffr = mkM1g. If we consider only the
block M1 , which does not rotate, the net torque must be zero,
which means that the normal force and the weight are separated
by a distance d. The torque of this couple must be balanced by the
torque from the tension and friction. If we take the point A as the axis, we have
mkM1gR0 - M1gd = 0, or - M1gd = - mkM1gR0.
For the entire system the tension is an internal force. Because the line of the friction force passes
through the center of the pulley, the net torque is produced by M2g and the couple from FN and M1g:
t = dL/dt;
M2gR0 - mkM1gR0 = [R0M1 + R0M2 + (I/R0)] dv/dt, which gives
a = (M2 - mkM1)g/[M1 + M2 + (I/R02)].
36. For the system of stick and bullet during the collision, angular momentum about the center of mass is conserved:
Li = Lf ;
mvi(1/4r) + 0 = mvi(1/4r) + Irodw ;
(3.0 g)(250 m/s)1/4(1.0 m) = (3.0 g)(160 m/s)1/4(1.0 m) + [(300 g)(1.0 m)2/12)]t,
which gives
w = 2.7 rad/s.
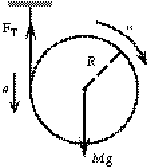
60. (a) Because the hoop is rolling down the string, the acceleration of
the center of mass is related to the angular acceleration:
a = aR.
For the linear motion of the center of mass we have
SF = Ma;
Mg - FT = Ma = MRa.
For the angular motion about the center of mass we have
St = dL/dt = Ia;
FTR = MR2a = MRa.
When we combine these equations, we get
a = a/R = 1/2g/R.
Thus we have
dL/dt = (MR2)(1/2g/R) = 1/2MRg, so L = 1/2MRgt.
(b) The tension in the string is
FT = Ma = M(1/2g) = 1/2Mg.
63. (a) If the thrown-off mass carries off no angular momentum, from conservation of angular momentum
for the star we have
Iiwi = Ifwf ;
2/5Mrs2w1 = 2/5(1/4M)rn2w2 , which gives
w2 = 4(rs/rn)2w1 = 4(7.0 x 105 km/10 km)2(1 rev/10 days)/(86,400 s/day) = 2.3 x 104 rev/s.
(b) If the thrown-off mass carries off & of the initial angular momentum, from conservation of
angular momentum for the star we have
1/4Iiwi = Ifwf ;
1/4(2/5Mrs2)w1 = 2/5(1/4M)rn2w2 , which gives
w2 = (rs/rn)2w1 = (7.0 x 105 km/10 km)2(1 rev/10 days)/(86,400 s/day) = 5.7 x 103 rev/s.
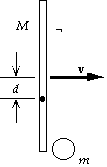
39. (a) We find the speed of the center of mass from the conservation of
linear momentum:
Mv + 0 = (M + m)vCM;
(200 kg)(18 m/s) = (200 kg + 50 kg)vCM , which gives vCM = 14 m/s.
(b) During the collision, angular momentum about the center of mass
will be conserved. We find the location of the center of mass relative
to the center of the beam:
d = m(1/2r)/(M + m) = (50 kg)1/2(2.0 m)/(200 kg + 50 kg) = 0.20 m.
When we use the parallel-axis theorem for the moment of inertia of
the beam, angular momentum conservation gives us
Li = Lf ;
Mvd + 0 = Itotalw = [(Mr2/12) + Md2 + m(1/2r - d)2]w;
(200 kg)(18 m/s)(0.20 m) = ((200 kg){[(2.0 m)2/12] + (0.20 m)2} + (50 kg)(1.0 m - 0.20 m)2)w,
which gives
w = 6.8 rad/s.