Chapter 14 Solutions

5.  (a)  We find the effective spring constant from the frequency:
      f1 = (k/m1)1/2/2p;
      10 Hz = [k/(0.60 x 10-3 kg)]1/2/2p, which gives k =       2.4 N/m.
  (b)  The new frequency of vibration will be
      f2 = (k/m2)1/2/2p = [(2.37 N/m)/(0.40 x 10-3 kg)]1/2/2p =       12 Hz.

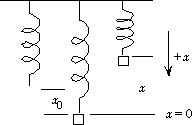
17.  We use a coordinate system with down positive.  With x0 positive, 
  at the equilibrium position we have 
    SF = -kx0 + mg = 0. 
  If the spring is compressed a distance x (so x is negative) from the 
  equilibrium position, we have
    SF = - k(x + x0) + mg. 
  When we use the equilibrium condition, we get
    SF = F = - kx.
  Note that x is negative, so the restoring force is positive (down).
  If we stretch the spring a distance x (so x is positive), we still have
    SF = - k(x + x0) + mg. 
  When we use the equilibrium condition, we get
    SF = F = - kx.
  Note that x is positive, so the restoring force is negative (up).

29.  We find the spring constant from the compression:
       k = F/x = (95.0 N)/(0.185 m) = 514 N/m.
   The kinetic energy will be maximum when the ball leaves the gun, 
   and thus equal to the initial potential energy:
     1/2mv2 = 1/2kx2;
    (0.200 kg)v2 = (514 N/m)(0.185 m)2, which gives v =       9.37 m/s.

31.  We can compare the two maximum potential energies:
    U1/U2 = 1/2k1A12/1/2k2A22 = (k1/k2)(A1/A2)2;
    10 = 2(A1/A2)2,   or         A1 = 2.24A2.

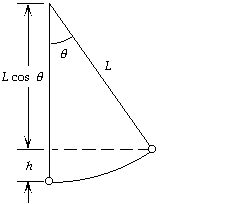
44.  We use energy conservation between the release point and the 
  lowest point:
    Ki + Ui = Kf + Uf ;
    0 + mgh = 1/2mv02 + 0,   or   v02 = 2gh = 2gL(1 - cos q).
  When we use a trigonometric identity, we get
  v02 = 2gL(2 sin2 1/2q).
  For a simple pendulum q is small, so we have sin 1/2q ==> 1/2q.  
  Thus we get
  v02 = 2gL2 (1/2q)2,   or        v0 = q(gL)1/2.

35.  For the collision of the bullet and block momentum is conserved:
      mv = (m + M)V,  so  V = mv/(m + M).
  The kinetic energy of the bullet and block immediately after the 
  collision is stored in the potential energy of the spring when the 
  spring is fully compressed:
    1/2(m + M)V2 = 1/2kA2;
    (m + M)[mv/(m + M)]2 = kA2;
    [(0.007870 kg)v]2/(0.007870 kg + 6.023 kg) = (142.7 N/m)(0.09460 m)2, 
  which gives 
    v =      352.6 m/s.

10.  The dependence of the frequency on the mass is 
    f = (k/m)1/2/2p.
  Because the spring constant does not change, we have
    f2/f = (m/m2)1/2;
    (0.48 Hz)/(0.88 Hz) = [m/(m + 1.25 kg)]1/2, 
  which gives 
    m =       0.53 kg.

16.  (a)  We find the derivatives of the given expression:
      x = a sin wt + b cos wt;
      dx/dt = wa cos wt - wb sin wt;
      d2x/dt2 = - w2a sin wt - w2b cos wt = - w2x.
    Thus Eq. 14-3 is satisfied if w2 = k/m.
  (b)  We use a trigonometric identity to expand Eq. 14-4:
      x = A cos (wt + f) = A(cos wt cos f - sin wt sin f).
    If we compare this to the given solution, we see that
      a = - A sin f,   and    b = A cos f.

22.  The impulse, which acts for a very short time, 
  will change the momentum of the mass, 
  giving it an initial velocity.  
  Because this occurs at the equilibrium position, 
  the velocity will be the maximum velocity v0.  Thus we have
      J = Dp = m Dv = mv0.
  The angular frequency is 
    w = (k/m)1/2, so v0 = Aw = A(k/m)1/2.
  The SHM starts at the equilibrium position, 
  x = 0 at t = 0, so we use a sine function:
      x = A sin wt = v0(m/k)1/2 sin (k/m)1/2t 
        = (J/m)(m/k)1/2 sin (k/m)1/2t = [J/(mk)1/2] sin (k/m)1/2t.

36.(a)  The period of the motion is independent of amplitude:
      T = 2p(m/k)1/2 
        = 2p[(0.650 kg)/(184 N/m)]1/2 =       0.373 s.
    The frequency is
      f = 1/T = 1/(0.373 s) 
        =       2.68 Hz.
  (b)  Because the mass is struck at the equilibrium position, 
    the initial speed is the maximum speed. We find the amplitude from
      v0 = Aw = 2pfA;
      2.26 m/s = 2p(2.68 Hz)A, 
    which gives 
      A =       0.134 m.
  (c)  The maximum acceleration is
      amax = w2A 
        = (2pf )2A = [2p(2.68 Hz)]2(0.134 m) 
        =        38.0 m/s2.
  (d)  Because the mass starts at the equilibrium position, 
    we have a sine function.  If we take the positive x-direction in the 
    direction of the initial velocity, we have
      x = A sin (wt) 
        = A sin (2pft) 
	= (0.134 m) sin [2p(2.68 Hz)t] 
	= (0.134 m) sin [(16.8 s-1)t].
  (e)  We find the total energy from the maximum kinetic energy:
      E = Kmax = 1/2mv02 
        = 1/2(0.650 kg)(2.26 m/s)2 =       1.66 J.
  (f)  We find the kinetic energy from the total energy:
      E = K + 1/2kx2;
      1.66 J = K + 1/2(184 N/m)[(0.40)(0.134 m)]2; 
    which gives 
      K =       1.40 J.

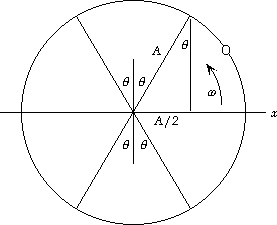
45.  This is most easily found from the associated circular 
  motion for SHM.  We see from the diagram that, out 
  of the 2p radians for a complete circular motion, the 
  total angle corresponding to the pendulum  being 
  between + 1/2A and - 1/2A is 4q.
  We find q from 
  sin q = 1/2A/A = 1/2, so q = p/6.
  Thus the fraction of time spent between + 1/2A and - 1/2A is
     fraction = 4(p/6)/2p = 1/3.

80.  The object will leave the surface when the maximum acceleration of the SHM 
   becomes greater than g, so the normal force becomes zero.  
   For the pebble to remain on the board, we have
   amax = w2A = (2pf)2A < g;
    [2p(5.0 Hz)]2A < 9.80 m/s2, which gives A < 9.93 x 10-3 m =      0.99 cm.