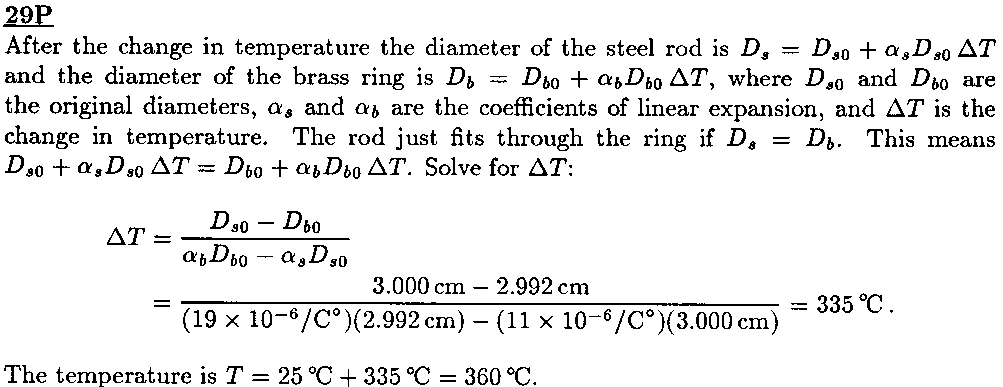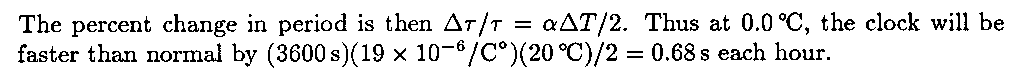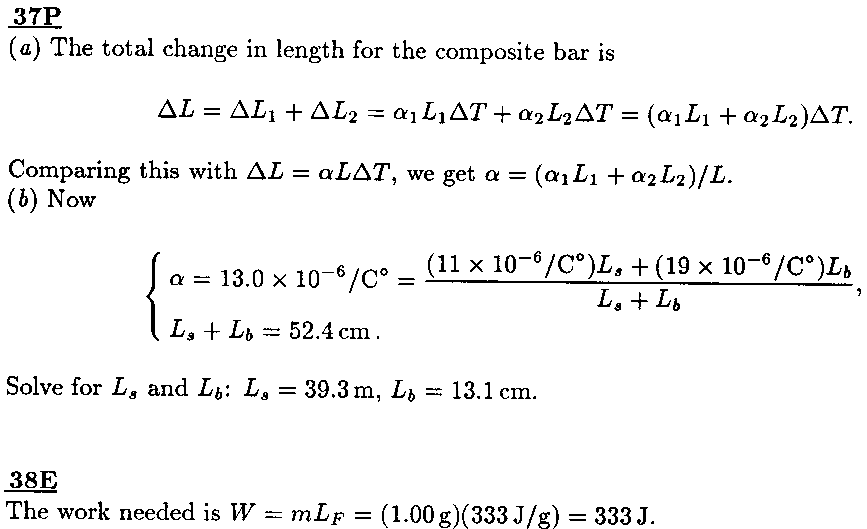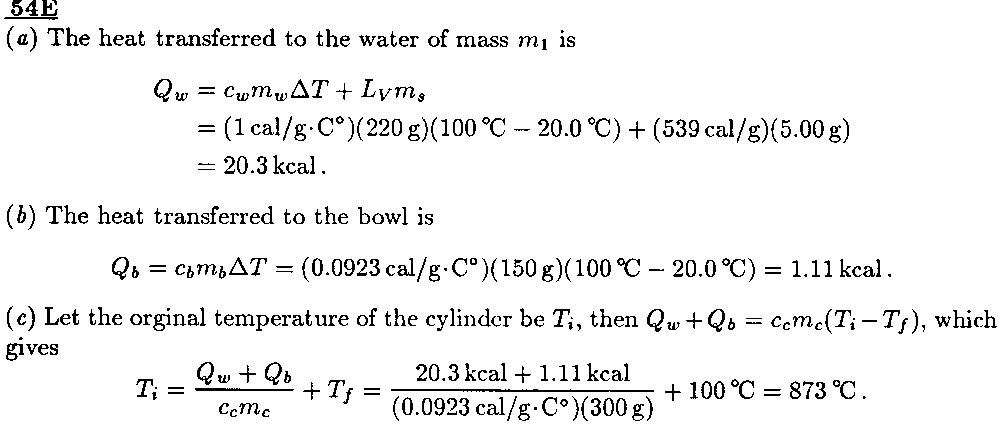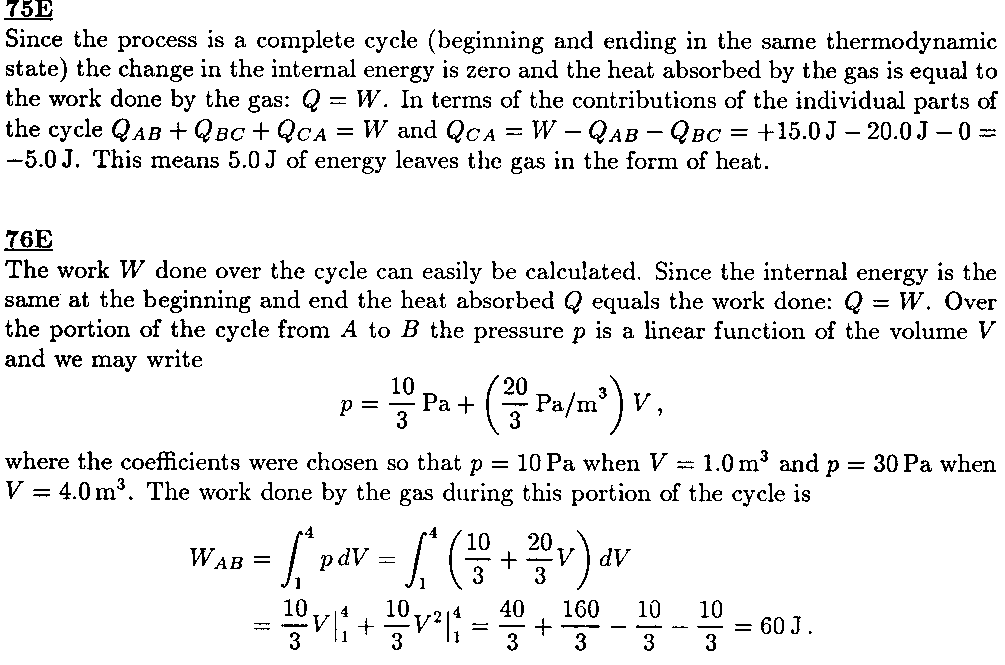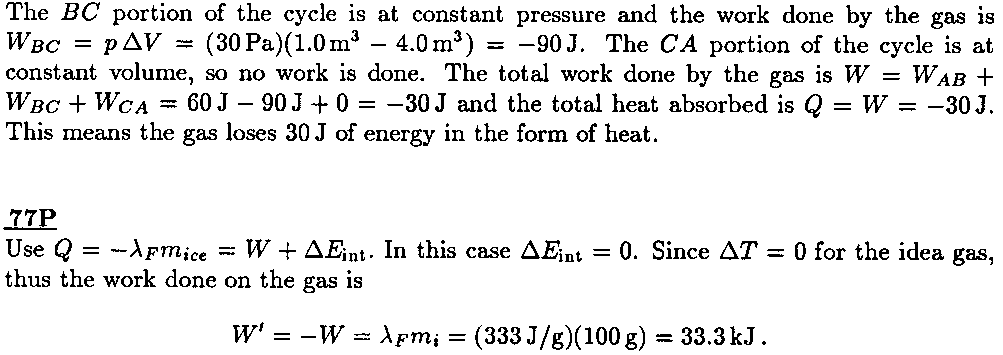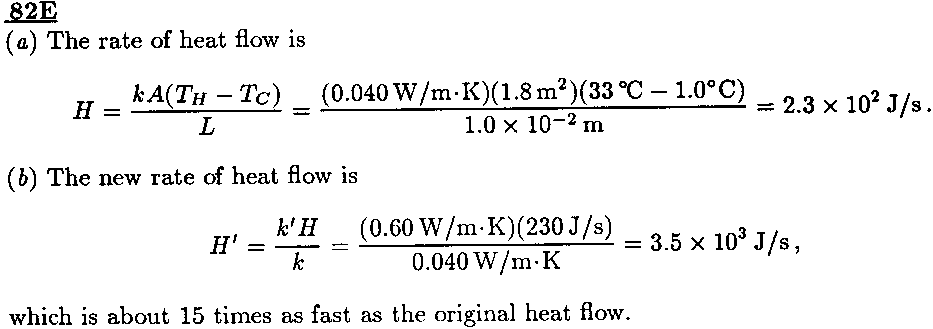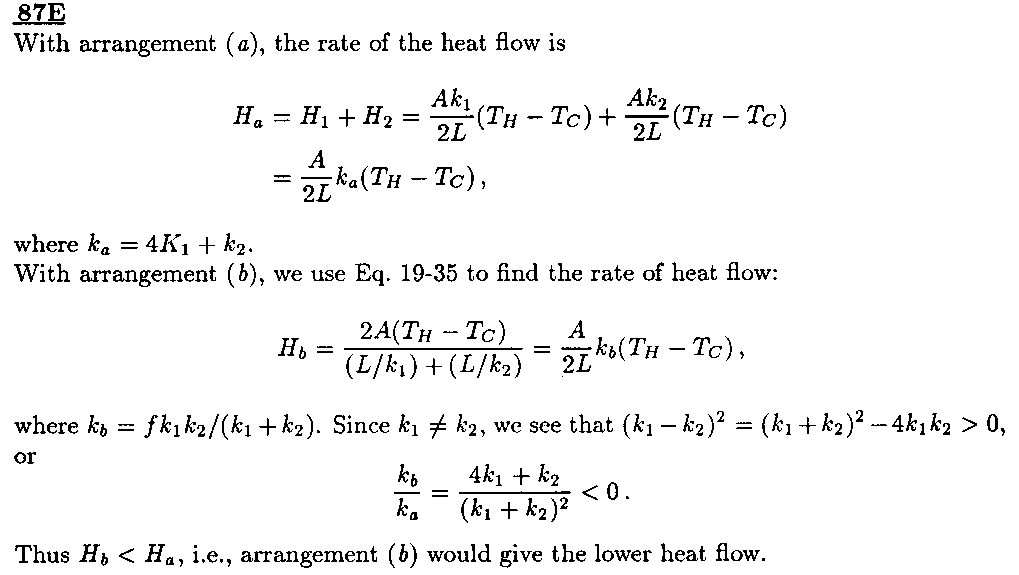Chapter 19
Homework Problems
(1,5,13,38) 4, 17, 29, 35, 37, 54, *** 75, 76, 77, 82, 87
Solutions
[1]
The temperature to which lambda = 0.107cm corresponds is T = 0.2898cm-K/0.107cm = 2.71 K
[4]
[The calibration of an unknown thermometer consists in finding
the straight line y = mx + b from two points. Here is the
longwinded explanation of that procedure in words.]
Let T_L be the temperature and p_L be the pressure in the left-hand
thermometer. Let T_R be the temperature and p_R the pressure in the
right-hand thermometer. According to the problem statement the
pressure is the same in the two thermometers when they are both
at the triple point of water. Take this pressure to be p_3. Write
Equation 19-5 for each thermometer:
T_L = (273.16K)(p_L/p_3) and
T_R = (273.16K)(p_R/p_3).
Subtract the second equation from the first to obtain:
T_L - T_R = (273.16K)([p_L-p_R] / p_3)
First take T_L=373.125K (the boiling point of water) and
T_R=273.16K (the triple point of water) then p__L - p_R = 120mm of Hg.
Solve:
373.125K - 273.16K = (273.16K)([120mm Hg/p_3)
for p_3. The result is p_3 = 328 mm of Hg. Now let T_L=273.16K
(the triple point of water and let T_R be the unknown temperature. The pressure
difference is p_L - P_R = 90.0 mm of Hg. Solve:
273.16K - T_R = (273.16K)(90mm of Hg/328mm of Hg)
for T_R. The result is T_R = 348K.
[5]
Let the reading of the temperature be T_F in Fahrenheit and T_C in Celcius.
Then we have two equations and two unknowns:
a) T_C = T_F/2
T_F = 9/5 T_C + 32
==> T_F = 320 F
And the second part just changes the first equation:
b) T_C = 2 T_F
===> T_F = -12.3 F.
[13]
The change in length of the rod is just:
dL = L alpha dT = (20cm)(11e-6/K)(50 C - 30 C)
= 4.4e-3 cm
[17]
(a) The coefficeint of linear expansion alpha fro the allow is
alpha = dL / L dT = (10.015 cm - 10.000 cm)/[(10.01cm)(100 C - 20.000 C)]
= 1.88e-5/C.
Thus from T = 100 C to T = 0 C we have
dL = L alpha dT = (10.015cm)(1.88e-5/C)(-100C) = -1.88e-2 cm.
The length at T = 0 C is therefore:
L' = L + dL = 10.015cm - 0.0188cm = 9.996cm.
(b) Let the temperature be T_x. Then from 20 C to T_x we have:
dL = 10.009cm - 10.000cm = alpha L dT = (1.88e-5/C)(10.000cm)dT,
giving dT = 48C. Thus T_x = 20 C + dT = 20 C + 48 C = 68 C.
[29]
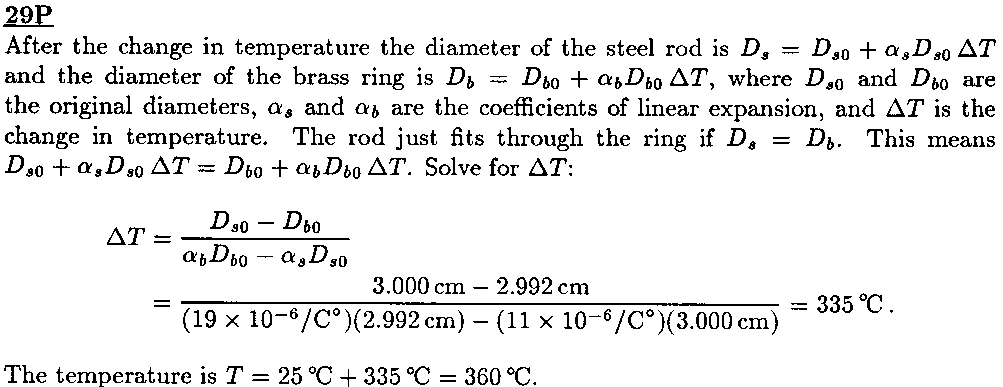
[35]

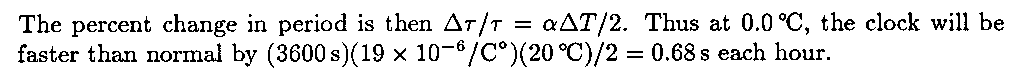
[37]
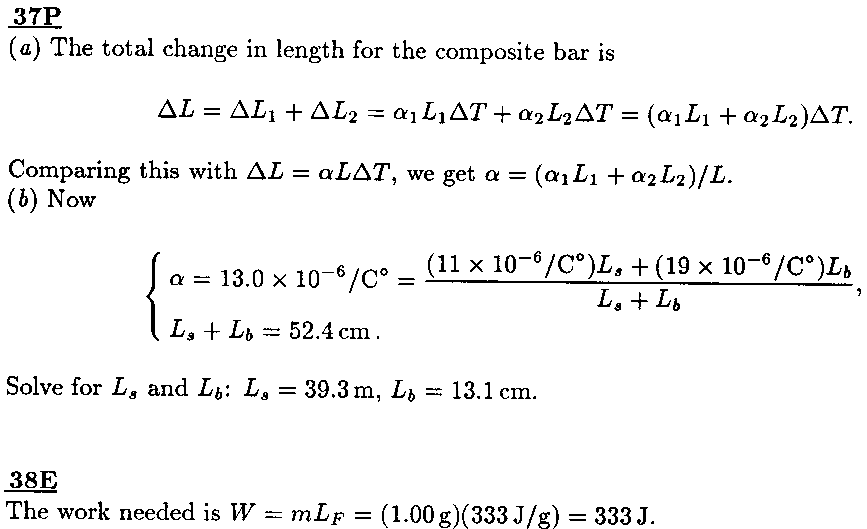
[54]
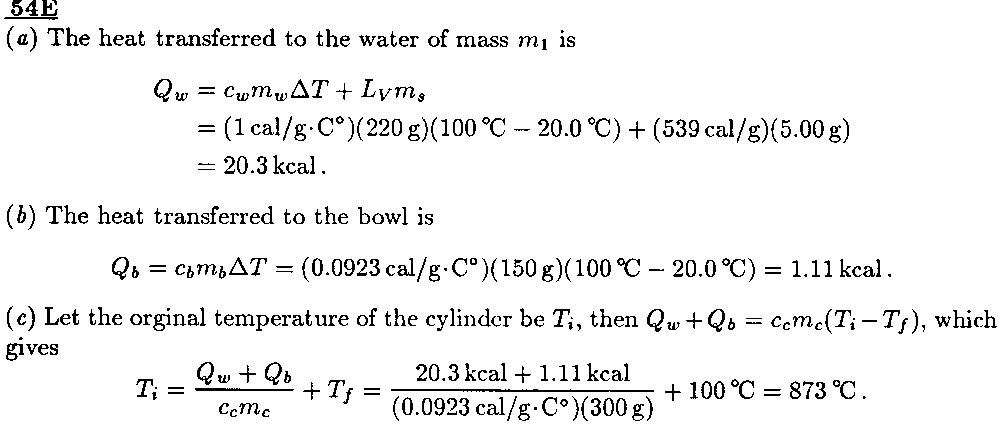
[75]
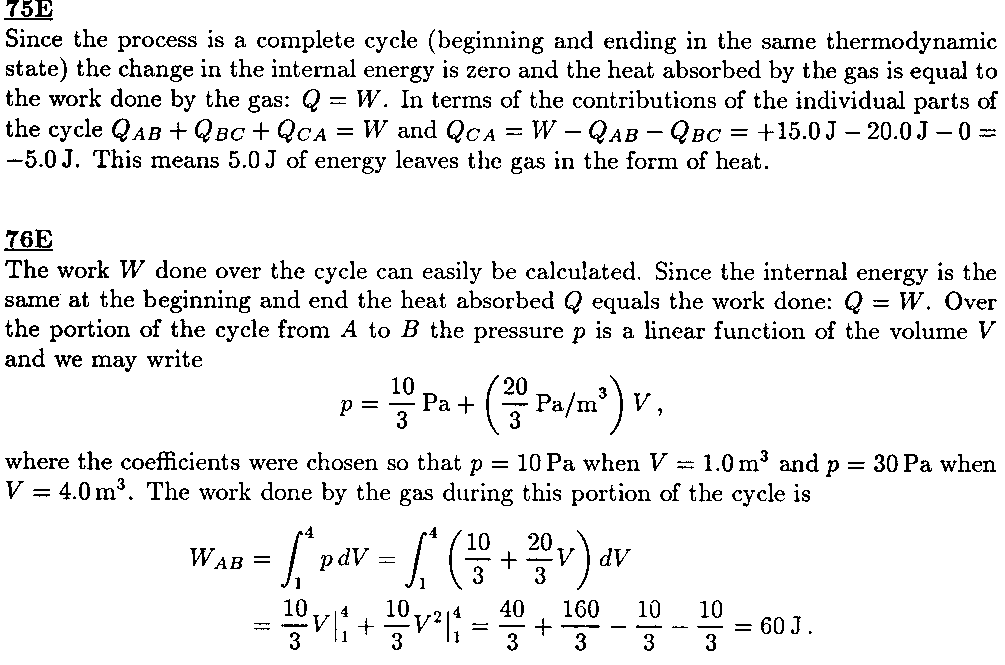
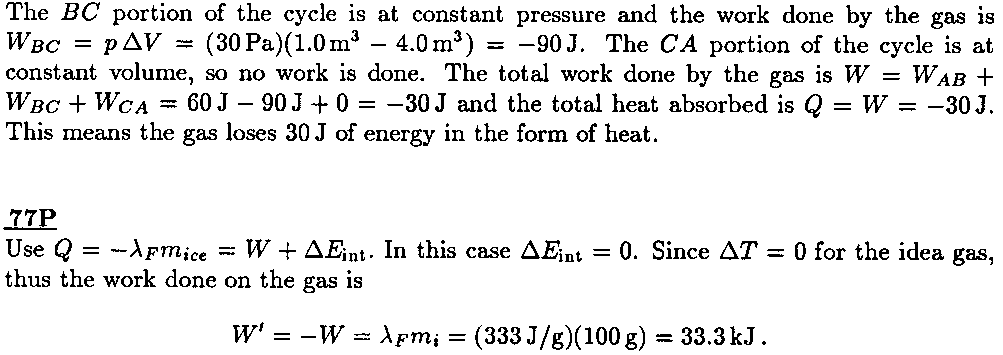
[82]
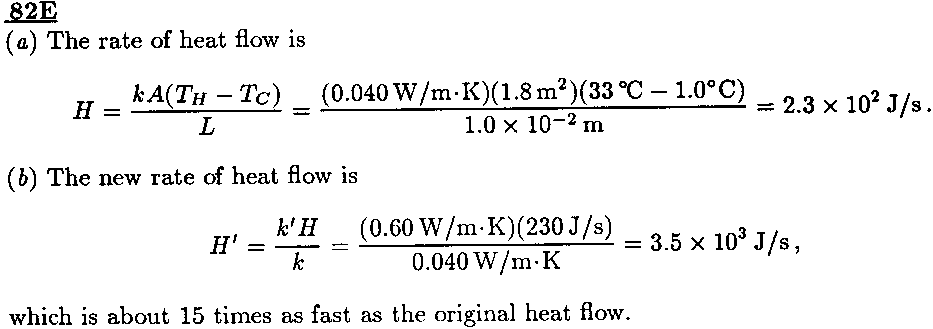
[87]
This problem has some strange notation, so I give a rough
idea of how to solve it. The key point is that a double layer
of insulator is a "compound" insulator, with a temperature
at the inside interface between the layers which is intermediate
between the hot and cold temperatures. Thus the derivation I did
in class is NOT correct, the correct answer is to use equation 19-35. In
part a), where we align like to like, the heat flow through each
half is just
Q_a = (k1/2 + k2/2) * A dT / L.
In part b) we must use the compound formula, or
Q_b = 2(k1 * k2)/(k1 + k2) * A dT/L
If we form the ratio of these two heats, we find
Q_a / Q_b = (k1 + k2) ( k1 + k2) / 4(k1 * k2)
= (k1^2 + k2^2)/(4 k1*k2) + 1/2.
Now if k1 = k2, this expression = 1, which means Qa = Qb, but
if k1 is a bit bigger or a bit smaller than k2, then this
expression is larger than 1, meaning that Qa > Qb. So if you want
to insulate your house, you are better off with two dissimilar
layers, than half of one type and half of the other.
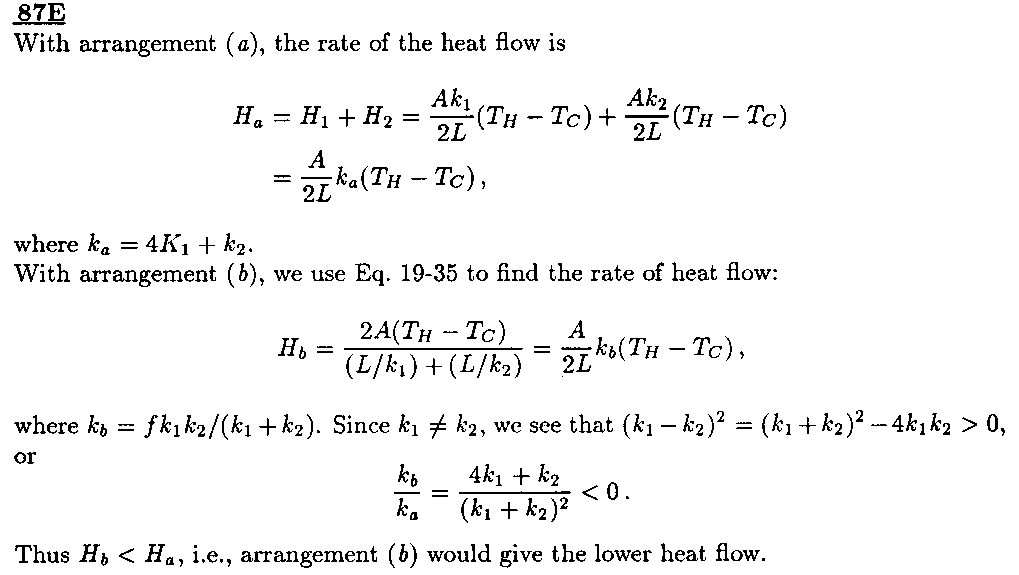
Go To Top