The UAH Spinning Terrella Accelerator

Abstract

Introduction

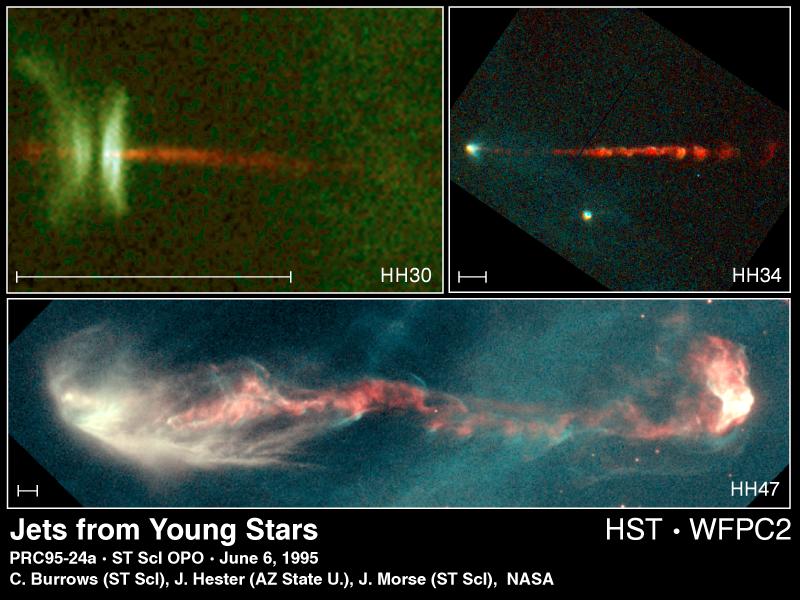
FIGURE 1: Two examples of astrophysical jets, galactic (top panel) and stellar (bottom panel).

Previous Work

Despite many diagnostics on their composition, speed, origin, distribution and the like, the driving mechanism that powers and maintains this dynamic system is still unknown. Early work in the 1970's focussed on the properties of a jet of relativistic fluid (e.g., Blandford82), but were found to be unconstrained and perhaps unstable. The evidence that magnetic fields were an important component of astrophysical jets came from two sources: the observations of synchrotron radiation, and the exquisite symmetries in the system which required a globally anisotropic medium. Thus work, done in the 1980's added magnetic fields to stabilize and direct the fluid flows, but inconsistently, for it did not allow the magnetofluid to produce magnetic fields itself. The recognition that magnetic fields are not just important components of astrophysical plasma jets, but a driving force has led in the 1990's to the development of magneto-hydrodynamic (MHD) 3-D models that self-consistently derive the flows and the magnetic fields.

Such a progression has occurred also in space plasma physics, with mature, large-scale, fully 3-D, non-dissipative MHD codes only now returning quantitative results. Despite their many successes and obvious future glory, one message is abundantly clear: they cannot describe the energetic plasma in the high-beta, inhomogeneous, large-gradient magnetic fields found at the centers of most magnetospheres. For example, the Earth's ring current, a ~6 mega-ampere current that encircles the Earth at a distance of ~3 R_e and produces a 100--400 nT decrease in the surface magnetic field during a major magnetic storm, is completely absent from all such MHD codes. That is, a current system that can hold 1/2 of the entire energy released in a magnetic storm is not itself derivable from MHD. Thus the holy grail of self-consistency, of agreement between particles and fields, slips through the mesh of all MHD models in the presence of large-gradient fields, such as those in the core engine of astrophysical jets.

But no negative criticism should be taken seriously until there is a positive and constructive solution offered. We therefore turn to the requirements, the constraints put on any astrophysical jet theory by the data.



Requirements

The characteristics of YSO jets and blazar jets obviously vary by orders of magnitude, but if we suppose that their similar characteristics reflect a similar mechanism, we can draw some far reaching conclusions. Such an assumption may be completely unwarranted of course, but like the apocryphal story of Newton and the apple unifying celestial mechanics with gravity, a unifying mechanism is inherently satisfying and therefore theoretically compelling. Quoting extensively from Pringle93 at the 1992 ``Astrophysical Jets Meeting'':


As I mentioned earlier, one point of this meeting is to draw together the experts on extragalactic jets and protostellar jets and to see if we can make common ground. The reason why one can try to do this, is that one can say similar things about the jet acceleration mechanism in both the extragalactic and the stellar cases... For example one can argue that these jets are not driven by radiation pressure, since in most instances the luminosities fall well below the Eddington luminosity..., and one can also argue that the jets are not pressure driven in view of the short cooling time for the jet material in the protostellar case, and the lack of dense and hot enough material to provide the jet-nozzle in the extragalactic case. In view of this, jet theorists have taken refuge in magnetic fields as the underlying acceleration and collimation mechanism for both the protostellar and the extragalactic jets... The basic ingredients of such a model are reasonably well agreed upon. They are: first, a central potential well, provided by the star in the protostellar case, and a massive black hole in the extragalactic case; second, an accretion disc, in order to provide the energy to power the jet and also the required symmetry for jet production; and third, a well-ordered magnetic field threading the disc in the perpendicular direction.

However, if we accept the hypothesis that both sets of jets are driven by the same underlying mechanism, then by use of Occam's Razor we can start to say things about what might or might not be required in the theorists' black box. For example, since jets are produced just as easily by protostars as by galactic nuclei, it is evident that neither black holes, nor relativistic effects are necessary for jet formation and any model which requires such effects can be discounted. Similarly jet formation requires neither a central star spinning at break-up speed...nor the existence of a boundary layer between disc and star..., since black holes can provide analogies to neither of these. Thus already we can start discarding some of the models that are around in the literature--not because they are necessarily wrong, but because they fail the test of simplicity (Occam's razor).


Pringle then goes on to make a list of characteristics which should be addressed in any jet theory. We abbreviate his list as follows:

The ratio of the jet speed to the escape velocity of the central object. Pringle derives a value of unity for YSO jets, and gamma factors of ``a few'' for AGN jets, which, he argues ``has significant implications for the magnetic model, the most important of which is that the disc knows where its center is, for that is where it produces the jet. Thus while self-similar models (e.g., Blandford82) are a valuable first step, they cannot be the full answer...the preferred model must be one which is able to select the central regions for jet production.''

The ratio of mass flux in the jet to disc accretion rate. Pringle argues that this should be no more than 30%, which implies again a central source, since if most of the mass in the accretion disk is expelled in the jet, then ``this would make star formation a remarkably inefficient process.''

The ratio of the radius at which collimation occurs to the radius of the central object. Pringle argues for ratios < 10,000 for YSO, and <100 for AGN. He concludes ``thus it is important to discover whether the mechanism which accelerates the jet material must also do its own collimation, or whether it can rely on some surrounding material to do the collimation for it.''

Variability. Pringle asks the question whether the variability in YSO and AGN jets are alike, ``It will be important to establish whether there are similarities, in timescales for variability, or degree, between the two types of jet. The theorists will need to ponder whether the variability is just due to variations in the central accretion rate (due perhaps to some property of the accretion disc) or whether it is due to some intrinsic property of the acceleration or collimation mechanisms.''

One- or two-sidedness. Pringle asks whether a jet theory should be symmetric (two-sided) or not (one-sided), and concludes that the data is leaning toward symmetry.

How big a [magnetic] field do we need? Pringle calculates the back pressure of a jet and compares it to the magnetic pressure. From this calculation he concludes ``that in general the poloidal field required to power the jet is insignificant as far as the structure of the disc is concerned. Thus from the disc's point of view, powering the jet requires only a weak magnetic field.''

Where does the [magnetic] field come from? Pringle discusses two possibilities, that the magnetic field is some global ambient field entrained in the disk and is advected inwards by accretion, or that the accretion disk itself produces internal magnetic fields through dynamo action. His calculations convince him ``that the disc itself is likely to contain fields with strengths much greater than the strength of the poloidal field required to drive the jet.''

Do all jets have accretion discs, and/or do all accretion discs have jets? Pringle argues that the data are ambiguous. ``In the extragalactic case, the problem with deciding if all discs have jets is obscured by the uncertainty of deciding whether all (active) galactic nuclei have discs. In the protostellar case, complete and unbiased surveys surveys are hard to come by, but it is beginning to look as if one can make the case that all objects in the rapid accretion phase, when they presumably have active accretion discs, display phenomena associated with collimated molecular outflows.''



More recent observations

Since that meeting, observations have poured in from recently opened observatories that have extended the multifrequency spectral range of blazars as well as improved the resolution of previously observed spectral ranges. At the International Workshop on Blazar Continuum Variability in 1996, a number of these new observations were reported that put tighter constraints on blazar models. R. Blandford (Blandford96) summarized the conference by making the points:

Hydrodynamic Jets The distance a hypersonic jet propagates in a constant homogeneous gas is the product of Mach number and jet diameter. However extragalactic jets are much longer than this, which Blandford attributes to possible power-law density variations in the ambient pressure away from the galaxy. However in the case of M87, he acknowleges that the jet must be collimated within 300 Schwarzschild radii, a task that only magnetic confinement can manage. He doesn't say whether that magnetic confinement contributes to the pressure gradient needed for extended jets.

Variability Much progress has been made in correlating multi-spectral data of variability, from radio to gamma-rays. In some cases strong correlations were found, such as visible and gamma-ray in other cases little correlation was found, such as radio and gamma-ray. But at least in some cases, there is strong evidence that travelling shocks within the relativistic jet are responsible for this cross-scale variability (Marscher96). There is also evidence from the inverse Compton models that the different frequency photons all derive from the same relativistic energy electrons (Ghisellini96). This suggests that the variability is not due to compositional changes in the jet (different energies, or species), rather it is due to inhomogeneities in the density and magnetic field of the jet (e.g., in shocks).

Accretion Disks Blandford says that there is general agreement that disks are essential to jet formation. "However we do not often have direct evidence of this at the radii where the jets are supposed to be formed, although there are more and more examples of rotating gas at larger radii." From which we infer that the data are hard to get, but support the hypothesis that all jets have disks.

Fundamental properties Blandford writes "If we reduce everything to fundamentals then a plausible set would be the mass of the [black] hole, the spin of the hole and the mass accretion rate. To this set of `intrinsic' parameters, I would add the extrinsic factors, the viewing angle and the nuclear star and gas densities."



Summary of Observations

From the reports, we can see that the new data of 1996 have confirmed and deepened the observational constraints known in 1992. The data all point to a relativistic jet arising from a system that includes an accretion disk, arising from the center of the system and collimated by magnetic forces. Recent studies by Zhang also imply that the core must be spinning at rather high rates.

Theory

Tests

Example: Earth Jets

At the Earth, the magnetosphere is drawn into a long comet tail by the flow of magnetized solar wind. As reconnection occurs along the flanks, a non-axisymmetric electric field is generated that moves ~1 keV plasma sunward by ExB drift from the tail. When this neutral plasma reaches the more dipolar region of the magnetosphere, within 8 R_e of the Earth, the magnetic gradients of the dipole itself cause the positive ions to move clockwise, and the negative electrons to move counter-clockwise around the Earth. This counter-streaming flow generates a current that almost forms a ring around the Earth. If some mechanism of nonadiabatic Earthward transport exists, then the ring is completed and the plasma is trapped. Both diffusion and time-dependent electric fields have been invoked to explain the growth in this trapped ring current during magnetic storms (Sheldon93a).

Note that charge separation occurs as soon as the dipole gradients are seen by the sunward convecting neutral plasma. It is generally assumed that the high conductivity of the cold plasma (assumed to be zero temperature, and therefore oblivious to magnetic gradients) allows the electrons to be redistributed in a way to maintain quasi-neutrality. Recent observations show that this assumption of sufficient cold plasma fails during a magnetic storm, and real charge separation may occur. Under these conditions, cold plasma from distant regions is required, and indeed accelerated to shield the space charge. POLAR made recent measurements of a 30 keV field-aligned potential drop during a small storm, that populated the ring current with accelerated ionospheric plasma (Sheldon98a). Thus the ring current can be explosively driven on timescales of minutes by upward ionospheric jets, as is evident in high time resolution magnetograms.



The Dipole Field

The theory depends crucially on the existence of a dipole magnetic field for all these astrophysical jets. For YSO, this is easy to invoke by analogy with our own Sun, but what about blazars? Why should they have any field at all, much less a dipole field? Certainly there is a great desire to invoke magnetic fields to solve the collimation and acceleration problems, as Pringle argues in the introduction, but there may be other reasons as well.

The physics of black holes is still an area of active research, with recent publications on the stability of magnetic fields in the vicinity of static black holes. But more importantly, recent work on black hole binaries, show that the black hole is probably spinning very rapidly, close to breakup speed Zhang99. We know that a black hole posesses three characteristics: mass, spin and charge. These rapidly spinning Kerr black holes may also be charged. Such a Kerr-Newman black hole will have a magnetic field that up to now, has never been calculated. Our expectation is that this will turn out to be the mechanism by which a blazar black hole minimizes its internal energy.

Regardless of speculations in general relativity, we know that the convective motion of plasma within a star produces magnetic fields by dynamo action. A similar process is occurring in the molten core of the Earth, which, surprisingly, is also a good approximation to MHD. In all these dynamo models, the dominant term in the magnetic field turns out to be the dipole term. Since the higher multipole moments in all such dynamo fields decay with distance more rapidly than the lowest, dipole term, there is emminently good reasons for arguing that a dipole field is generated wherever dynamo theory is applicable. It is our suspicion that independent of whether a black hole produces a dipolar field, dynamo theory should be applicable to the accretion disk, and should produce a dipolar field. Even a simple toroidal current at the inner edge of the accretion disk would appear as a dipole field from a sufficient distance. Thus we argue that several plausible mechanisms exist that can explain the ubiquitous nature of a dipole magnetic field in the vicinity of AGNs and YSOs.



The Jet Velocity

We see two processes limiting the charge separation electric field, a parallel and perpendicular limit. As the space charge builds up, the ions are repelled and mirror deeper down the field line. In the case of a protostellar object, this brings the ions closer to the dense plasma of the star itself, and eventually cold electrons or recombination destroy the space charge. In the case of a blazar black hole, the mirror force is exceptionally strong because the compact size of the hole permits a large convergence of field lines, so we would expect a much large space charge to develop. Eventually Hawking radiation or loss to the Schwarzschild boundary would destroy the space charge. This is the parallel limit.

The perpendicular limit occurs when second order effects become important in the drift of the charged particles. Adjacent to the space charge will be flux tubes with no space charge, yet they will ``see'' this space charge and hence collect plasma attempting to provide a ``Debye'' shielding to the space charge. Electrons will be preferentially collecting at the equator of this neighboring flux tube as they find a potential well generated by the adjacent space charge. Physically this produces a large perpendicular electric field and electric field gradient, which itself causes drifts. This is analogous to Pedersen and Hall conductivities in the ionosphere. The electric field causes a Hall conductivity, but the gradient in electric field generates a Pedersen conductivity, which can discharge the space charge.

Following Rothwell95,
dV_x/dt = e/M (E_x(x(t)) + V_y B)
dV_y/dt = -e/M V_x B
which can be combined,
d²V_x/dt² + (omega² - e/M dE_x/dx)V_x = 0
where we define,
Omega² = omega² - e/M dE_x/dx

Rothwell writes, ``The main effect of a spatial gradient in E_x is to modify the gyrofrequency, where the symbol omega=eB/M denotes the gyrofrequency. It is immediately seen that if Omega²<+0 then V_x has an exponential rather than an oscillatory solution. That is, if the electric field gradient is too steep the ions become locally untrapped.''

If space charge can be made large enough, we will have available MeV to GeV potentials. Thus the ability for this positive space charge to accelerate GeV protons (Lorentz factors of a few) and GeV electrons (Lorentz factors of 10³) depends on the discharge or recombination mechanisms available. From this equation, we can see that if our space charge is limited by this electric-field-gradient conductivity, then a 10¹⁷ cm magnetosphere (Mkn421) with a field of 0.04 G will support a potential of 1 GeV, giving nearly the Lorentz factors required. This happy coincidence lends support to the validity of this approach.



The Jet Formation

How would such a magnetic field-aligned beam of particles become so pencil thin? Well we need to know more about the mechanism before we understand fully what is happening, but here is our best guess. The more massive ions near the equator of the dipole field arising from the accretion disk will generate a positive space charge, which the rapidly moving electrons cannot quite compensate, so that a negative charge accumulates near the poles of the AGN. This situation forms a quadrupolar electric field of MV to GV intensity. Now beams of positive charges (protons? positrons?) are quickly accelerated from near the center of the system at the ``ionosphere'' and as they accelerate upward the magnetic field weakens to the point that they are no longer magnetically confined. Their momentum carries them up over the pole where they are both magnetically and electrically focussed to a narrow beam. Presumably they become neutralized at some point by scattering electrons from the ambient medium and ``dragging'' them along with the beam. The key point is that most of the focussing is done early on, in the vicinity of their acceleration by the AGN magnetic dipole field.

A second factor is the bending of the magnetic field by this jet. This requires self-consistency between the particles and the field, and is best modelled with MHD. So at some distance from the dipole center, MHD becomes a valid approximation and can simulate the self-focussing that occurs as charged plasma ``drag'' the field lines and produce a nozzle.



Non-neutral Plasma

One of the major obstacles in this theory is the predication of a non-neutral space charge. At a fundamental level, the physics of trapped, non-neutral plasmas has only been recently explored in the context of positron traps (Hansen95), and no one has postulated it for space plasmas. Thus it is very important to demonstrate that a dipole magnetic field has the capability to trap non-neutral plasmas. In the Malmberg trap used by Hansen and Fajans, a strong cylindrical magnetic field ``bottle'', with endcaps held at high voltage, is made to circulate via a time-dependent azimuthal field. In principle, this has a striking similarity to a rotating magnetic dipole field, where the surface charge on the dipole acts as a endcap field. The difference is that Fajans is using the electric potential to confine the space charge, whereas our application uses the space charge to produce the encap fields. As a very suggestive corollary, Carl McIlwain (private communication, 1995) found that the electric potential model, E5W, that best fit his ATS-5 satellite data included a monopole term for the Earth. Thus the missing link in this theory appears to be a conclusive test of the ``dipole charging'' of a spinning magnet in the presence of a plasma source, a laboratory experiment.

Experiment

FIGURE 2: The laboratory setup, and a high voltage plasma discharge in a tenuous, 1 Torr atmosphere.

Future Work

Acknowlegements

Bibliography

• Alfven, H. and C.-G. Falthammar. Cosmical Electrodynamics, Fundamental Principles. Clarendon, Oxford, 1963.
• Blandford, R.D. and D.G. Payne. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. astr. Soc., 199, 883--903, 1982.
• Blandford, R. Present and future blazar variability (i). In H.R. Miller, J.R. Webb, and J.C. Noble, editors, Blazar Continuum Variability, Conference Series, Vol 110, pages 475--4882. Astronomical Society of the Pacific, 1996.
• Ghisellini, G. and L.Maraschi. High energy variability and blazar emission models (i). In H.R. Miller, J.R. Webb, and J.C. Noble, editors, Blazar Continuum Variability, Conference Series, Vol 110, pages 436--449. Astronomical Society of the Pacific, 1996.
• C. Hansen and J. Fajans, Dynamic and Debye shielding and antishielding in magnetized, collisionless plasmas, Phys. Rev. Lett., 74, 1995.
• Marscher, A.P. Variability of the non-thermal emission in the jets of blazars (i). In H.R. Miller, J.R. Webb, and J.C. Noble, editors, Blazar Continuum Variability, Conference Series, Vol 110, pages 248--261. Astronomical Society of the Pacific, 1996.
• Pringle, J.E. Cosmogony of stellar and extragalactic jets. In Astrophysical Jets: Space Telescope Science Institute Symposium Series, pages 1--12. Cambridge University Press, 1993.
• P. L. Rothwell and M. B. Silevitch and L. P. Block and C.-G. Falthammer, Single Ion Dynamics and Multiscale Phenomena, Edited by J. L. Horwitz and N. Singh and J. L. Burch, Cross-Scale Coupling in Space Plasmas, Geophysical Monograph 93, AGU, 1995.
• Sheldon, R.B. and D.C. Hamilton. Ion transport and loss in the earth's quiet ring current 1. data and standard model. J. Geophys. Res., 98, 13,491--13,508, 1993.
• R. B. Sheldon and H. E. Spence, A New Magnetic Storm Model, Geospace Mass and Energy Flow: Results from the International Solar-Terrestrial Physics Program, Edited by J. Horwitz, AGU, Washington, D.C., 1998.
• R. B. Sheldon and H. E. Spence and J. F. Fennell, Observation of 40 keV Field-Aligned Ion Beams, Geophys. Res. Lett., 25, 1617-1620, 1998.
• Whipple, Jr, E.C. The signature of parallel electric fields in a collisionless plasma. J. Geophys. Res., 82, 1525, 1977.
• Williams, D.L., B.H. Mauk, R.E. McEntire, E.C. Roelof, T.P. Armstrong, B.Wilken, J.G. Roederer, S.M. Krimigis, T.A. Fritz, and L.J. Lanzerotti. Electron beams and ion composition measured at io and in its torus. Science, 274, 401--403, 1996.
• Zhang, Shuang-Nan, private communication, 1999.