| (4) |
Our initial populations can be described by a phase density for electrons
and ions as follows:
| (4) |
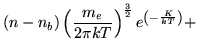 |
(5) | ||
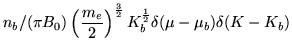 |
If we carry out the zeroeth moment integral to find the quasi-neutrality
condition according to the Whipple prescription, we arrive at a similar
equation,
By the appropriate asymptotic expansions, we can characterize the solution
as a function of ![]() . Let
. Let ![]() be small and positive, corresponding to a
few volt (few
be small and positive, corresponding to a
few volt (few ![]() ) potential needed to shift the thermal plasma such that
the ion beam is neutralized.
) potential needed to shift the thermal plasma such that
the ion beam is neutralized.
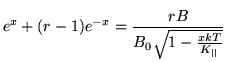 |
(10) | ||
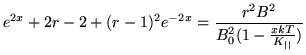 |
(11) |
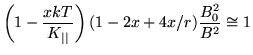 |
(12) | ||
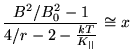 |
(13) |
From this expansion, we see that when we are at the equator, ![]() and the potential is zero, as defined by Whipple. Furthermore, since
and the potential is zero, as defined by Whipple. Furthermore, since ![]() and
and
![]() is positive, the denominator is always
positive definite. Thus the potential quadratically increases with
is positive, the denominator is always
positive definite. Thus the potential quadratically increases with
![]() away from the equator, which means a proton will be confined to
the equator, but an electron will be accelerated away from the equator.
This solution produces the well-known potential of several
away from the equator, which means a proton will be confined to
the equator, but an electron will be accelerated away from the equator.
This solution produces the well-known potential of several ![]() along the field line
[15] as documented by Whipple [5].
Heuristically, this is all the voltage needed to shift massive numbers of
cold electrons to the ion mirror point and shield the ion charge.
along the field line
[15] as documented by Whipple [5].
Heuristically, this is all the voltage needed to shift massive numbers of
cold electrons to the ion mirror point and shield the ion charge.